题目内容
已知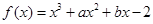 的图象过点
的图象过点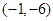 ,且函数
,且函数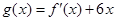 的图象关于
的图象关于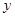 轴对称;
轴对称;
(1)求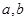 的值及函数
的值及函数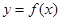 的单调区间;
的单调区间;
(2)求函数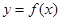 极值.
极值.
【答案】
(1) a=-3,b="0." (2) f(x)(-∞,0),(2,+∞)上是增加的;f(x)在(0,2)上是减少的.
【解析】
试题分析:(1)由函数f(x)图象过点(-1,-6),得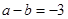 ,①
,①
由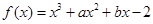 ,得
,得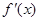 =3x2+2ax+b, (2分)
=3x2+2ax+b, (2分)
则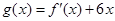 =3x2+(2a+6)x+b;
=3x2+(2a+6)x+b;
而g(x)图象关于y轴对称,所以-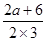 =0,所以a=-3, (3分)
=0,所以a=-3, (3分)
代入①得b=0. 于是f′(x)=3x2-6x=3x(x-2). (5分)
由f′(x)>0得x>2或x<0,
故f(x)(-∞,0),(2,+∞)上是增加的;(7分)
由f′(x)<0得0<x<2, 故f(x)在(0,2)上是减少的. (7分)
(2)由(1)得f′(x)=3x(x-2),
令f′(x)=0得x=0或x=2.
当x变化时,f′(x)、f(x)的变化情况如下表: (正确列出下表得3分)
|
x |
(-∞.0) |
0 |
(0,2) |
2 |
(2,+ ∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
|
极大值 |
|
极小值 |
|
由此可得:有极大值f(0)=-2,有极小值f(2)=-6,(12分)
考点:函数的奇偶性;利用导数研究函数的单调性;利用导数研究函数的极值。
点评:极值点的导数为0,但导数为0的点不一定是极值点。在大题中,我们一定要注意求函数极值的步骤。属于典型题型。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
