题目内容
已知点 、
、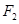 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于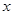 轴的直线与双曲线交于
轴的直线与双曲线交于 、
、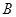 两点,若
两点,若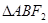 为锐角三角形,则该双曲线的离心率
为锐角三角形,则该双曲线的离心率 的取值范围是
的取值范围是
A.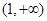 B.
B. C.(1,2) D.
C.(1,2) D.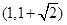
【答案】
D
【解析】
试题分析:在双曲线 (a>0,b>0)中,
(a>0,b>0)中,
令x="-c"
得,y=± ,∴A,B两点的纵坐标分别为±
,∴A,B两点的纵坐标分别为± .
.
由 是锐角三角形知,
是锐角三角形知, ,tan
,tan =
= <tan
<tan =1,
=1,
∴ ,
, ,解得
,解得 .
.
又 e>1,∴1<e< ,故选D.
,故选D.
考点:本题主要考查双曲线的几何性质,三角形性质。
点评:中档题,本题综合性较强,充分借助于三角形特征,确定得到角的范围,从而得到a,b,c的不等关系式。一般的,对圆锥曲线的几何性质的考查,往往涉及a,b,c,e,p。

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 、
、 分别是双曲线
分别是双曲线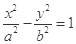 的左、右焦点,过
的左、右焦点,过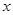 轴的直线与双曲线交于
轴的直线与双曲线交于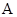 、
、 两点,若
两点,若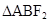 为锐角三角形,则该双曲线的离心率
为锐角三角形,则该双曲线的离心率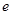 的取值范围是____________.
的取值范围是____________. 、
、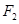 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过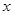 轴的直线与双曲线交于
轴的直线与双曲线交于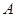 、
、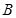 两点,若
两点,若 为锐角三角形,则该双曲线的离心率
为锐角三角形,则该双曲线的离心率 的取值范围是
的取值范围是 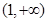 B.
B. C.(1,2) D.
C.(1,2) D.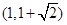
 ,
, 分别是双曲线
分别是双曲线 的左、右焦点,过F1且垂直于
的左、右焦点,过F1且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 ,
, 两点,若
两点,若 是锐角三角形,则该
是锐角三角形,则该 ,
, 分别是双曲线
分别是双曲线 的左、右焦点,过F1且垂直于
的左、右焦点,过F1且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 ,
, 两点,若
两点,若 是锐角三角形,则该
是锐角三角形,则该