题目内容
若不等式组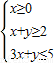 所表示的平面区域被直线y=kx+2分成面积相等的两部分,则k的值为( )
所表示的平面区域被直线y=kx+2分成面积相等的两部分,则k的值为( )A.4
B.1
C.2
D.3
【答案】分析:先画出不等式组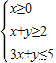 所表示的平面区域,求出平面区域的面积以及在直线y=kx+2 一侧的面积;再结合平面区域被直线y=kx+2 分为面积相等的两部分即可求出k的值.
所表示的平面区域,求出平面区域的面积以及在直线y=kx+2 一侧的面积;再结合平面区域被直线y=kx+2 分为面积相等的两部分即可求出k的值.
解答: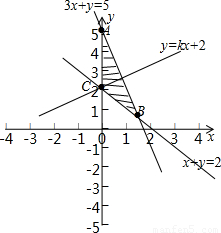 解:不等式组
解:不等式组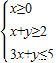 所表示的平面区域可以画出来:如下图
所表示的平面区域可以画出来:如下图
可行域为S△ABC,不等式组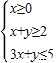 所表示的平面区域被直线y=kx+2分成面积相等的两部分,
所表示的平面区域被直线y=kx+2分成面积相等的两部分,
直线y=kx+2恒过点(0,2),要使直线y=kx+2将S△ABC,面积相等的两部分,
可知直线过点A与B的中点,
A(0,5),B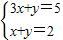 解得B(
解得B( ,
, ),
),
可得A、B的中点为( ,
,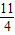 )将其代入直线y=kx+2,
)将其代入直线y=kx+2,
可得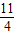 =k×
=k× +2,∴k=1
+2,∴k=1
故选B;
点评:本题主要考查二元一次不等式(组)与平面区域.考查学生的数形结合思想的应用,计算能力以及分析问题的能力;
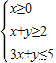 所表示的平面区域,求出平面区域的面积以及在直线y=kx+2 一侧的面积;再结合平面区域被直线y=kx+2 分为面积相等的两部分即可求出k的值.
所表示的平面区域,求出平面区域的面积以及在直线y=kx+2 一侧的面积;再结合平面区域被直线y=kx+2 分为面积相等的两部分即可求出k的值.解答:
 解:不等式组
解:不等式组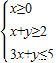 所表示的平面区域可以画出来:如下图
所表示的平面区域可以画出来:如下图可行域为S△ABC,不等式组
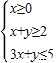 所表示的平面区域被直线y=kx+2分成面积相等的两部分,
所表示的平面区域被直线y=kx+2分成面积相等的两部分,直线y=kx+2恒过点(0,2),要使直线y=kx+2将S△ABC,面积相等的两部分,
可知直线过点A与B的中点,
A(0,5),B
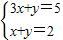 解得B(
解得B( ,
, ),
),可得A、B的中点为(
 ,
,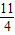 )将其代入直线y=kx+2,
)将其代入直线y=kx+2,可得
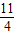 =k×
=k× +2,∴k=1
+2,∴k=1故选B;
点评:本题主要考查二元一次不等式(组)与平面区域.考查学生的数形结合思想的应用,计算能力以及分析问题的能力;

练习册系列答案
相关题目
 所表示的平面区域被直线
所表示的平面区域被直线 所表示的平面区域被直线
所表示的平面区域被直线 所表示的平面区域被直线
所表示的平面区域被直线 分为面积相等的两部分,则
分为面积相等的两部分,则 的值是( )
的值是( ) B.
B. C.
C. D.
D.
 所表示的平面区域被直线
所表示的平面区域被直线 分为面积相等的两部分,则k的值是
分为面积相等的两部分,则k的值是 B.
B. C.
C. D.
D. [
[ 所表示的平面区域被直线
所表示的平面区域被直线 分为面积相等的两部分,
分为面积相等的两部分, 的值是
的值是  B.
B.  C.
C. D.
D. 