题目内容
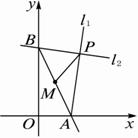
过点P(2,4)作两条互相垂直的直线l1、l2,l1交x轴于A点,l2交y轴于B点,求线段AB中点M的轨迹方程.
答案:
解析:
提示:
解析:
|
解:设M(x,y),连结PM,∵l1⊥l2且M为AB中点, ∴|MP|= ∵|OM|= 即 化简得x+2y-5=0. 故所求点M的轨迹方程是x+2y-5=0. |
提示:
|
对问题的考虑若从正面不易解决,可换个角度去思考,如△ABC中的角与倾斜角建立关系再与斜率联系,易于建立已知条件与方程的转换关系.同时应注意题目中的隐含条件|AB|>|AC|的应用,寻求最佳解的方法,培养严密的思维习惯. |

练习册系列答案
相关题目