题目内容
过点P(2,3)作直线l分别与x轴的正半轴和y轴的正半轴交于A(a,0),B(0,b)两点.
(1)求|OA|+|OB|的最小值.
(2)当△AOB(O为原点)的面积S最小时,求直线l的方程,并求出S的最小值.
(3)当|PA|•|PB|取得最小值时,求直线l的方程.
(1)求|OA|+|OB|的最小值.
(2)当△AOB(O为原点)的面积S最小时,求直线l的方程,并求出S的最小值.
(3)当|PA|•|PB|取得最小值时,求直线l的方程.
分析:(1)过P作PC⊥x轴于点C,PD⊥y轴于点D,设∠PAO=θ,利用解直角三角形知识算出|AC|=
且|BD|=2tanθ,从而将|OA|+|OB|表示为关于tanθ的式子,再利用基本不等式加以计算,即可求出|OA|+|OB|的最小值;
(2)设AB的方程为
+
=1(a>0,b>0),可得
+
=1,利用基本不等式算出ab≥24,可得当且仅当a=4且b=6时,△AOB的面积S有最小值为12,进而算出此时的直线l方程;
(3)由(1)的结论得|PA|=
且|PB|=
,利用二倍角的正弦公式算出|PA|•|PB|=
,由正弦函数的值域可得当θ=45°时,|PA|•|PB|取最小值12.而此时直线的倾斜角为135°,得到斜率为-1,利用点斜式方程列式,化简可得直线l的方程.
| 3 |
| tanθ |
(2)设AB的方程为
| x |
| a |
| y |
| b |
| 2 |
| a |
| 3 |
| b |
(3)由(1)的结论得|PA|=
| 3 |
| sinθ |
| 2 |
| cosθ |
| 12 |
| sin2θ |
解答:解:设∠PAO=θ,则可得θ∈(0,
),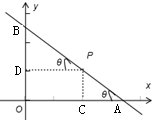
过P作PC⊥x轴于点C,PD⊥y轴于点D,
则Rt△PDB中,tanθ=
,可得|BD|=|PD|tanθ=2tanθ,
cosθ=
,可得|PB|=
=
,
同理,在Rt△PAC中,有|AC|=
=
,|PA|=
,
(1)|OA|+|OB|=|OC|+|AC|+|OD|+|BD|=5+
+2tanθ,
∵θ∈(0,
),得tanθ>0,
∴
+2tanθ≥2
=2
,可得当且仅当tanθ=
时,等号成立.
由此可得|OA|+|OB|=5+
+2tanθ的最小值为5+2
;
(2)设直线AB的方程为
+
=1(a>0,b>0),
∵点P(2,3)在直线上,∴
+
=1,
由基本不等式,得1=
+
≥2
=
,当且仅当a=4且b=6时,等号成立,
∴ab≥24,可得△AOB的面积S=
ab≥12,
因此△AOB的面积S的最小值为12,
此时的直线方程为
+
=1,即3x+2y-12=0.
(3)∵|PA|=
,|PB|=
,
∴|PA|•|PB|=
•
=
,
∴当2θ=90°,即θ=45°时,|PA|•|PB|取最小值12,
此时,直线的倾斜角为135°,斜率为-1,
直线l的方程为y-3=-1(x-2),化为一般式可得x+y-5=0.
| π |
| 2 |

过P作PC⊥x轴于点C,PD⊥y轴于点D,
则Rt△PDB中,tanθ=
| |BD| |
| |PD| |
cosθ=
| |PD| |
| |PB| |
| |PD| |
| cosθ |
| 2 |
| cosθ |
同理,在Rt△PAC中,有|AC|=
| |PC| |
| tanθ |
| 3 |
| tanθ |
| 3 |
| sinθ |
(1)|OA|+|OB|=|OC|+|AC|+|OD|+|BD|=5+
| 3 |
| tanθ |
∵θ∈(0,
| π |
| 2 |
∴
| 3 |
| tanθ |
|
| 6 |
| ||
| 2 |
由此可得|OA|+|OB|=5+
| 3 |
| tanθ |
| 6 |
(2)设直线AB的方程为
| x |
| a |
| y |
| b |
∵点P(2,3)在直线上,∴
| 2 |
| a |
| 3 |
| b |
由基本不等式,得1=
| 2 |
| a |
| 3 |
| b |
|
|
∴ab≥24,可得△AOB的面积S=
| 1 |
| 2 |
因此△AOB的面积S的最小值为12,
此时的直线方程为
| x |
| 4 |
| y |
| 6 |
(3)∵|PA|=
| 3 |
| sinθ |
| 2 |
| cosθ |
∴|PA|•|PB|=
| 3 |
| sinθ |
| 2 |
| cosθ |
| 12 |
| sin2θ |
∴当2θ=90°,即θ=45°时,|PA|•|PB|取最小值12,
此时,直线的倾斜角为135°,斜率为-1,
直线l的方程为y-3=-1(x-2),化为一般式可得x+y-5=0.
点评:本题给出直线经过定点,求满足特殊条件的直线方程,着重考查了直线的基本量与基本形式、三角形面积的计算和基本不等式求最值等知识,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).