题目内容
设a∈R,解下列关于x的不等式|1-
解法一:当a≤0时,原不等式的解集为![]() .
.
当a>0时,![]() <a即(x-1)2<a2x2,即(a2-1)x2+2x-1>0.
<a即(x-1)2<a2x2,即(a2-1)x2+2x-1>0.
①当a>1时,原不等式可化为[(a+1)x-1][(a-1)x+1]>0.
∴原不等式的解集为{x|x>![]() 或x<
或x<![]() }.
}.
②当0<a<1时,原不等式可化为[(1+a)x-1][(1-a)x-1]<0.
∴原不等式的解集为{x|![]() <x<
<x<![]() }.
}.
③当a=1时,原不等式可化为2x-1>0.
∴原不等式的解集为{x|x>![]() }.
}.
综上,当a≤0时,原不等式的解集为![]() ;
;
当a>1时,原不等式的解集为{x|x>![]() 或x<
或x<![]() };
};
当a=1时,原不等式的解集为{x|x>![]() };
};
当0<a<1时,原不等式的解集为{x|![]() <x<
<x<![]() }.
}.
解法二:当a≤0时,原不等式的解集为![]() .
.
当a>0时,原不等式等价于-a<1-![]() <a,1-a<
<a,1-a<![]() <a+1,
<a+1,
∴![]() 或
或![]()
①若0<a<1时,原不等式等价于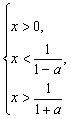 或
或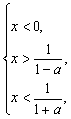
即{x|![]() <x<
<x<![]() }.
}.
②若a=1时,原不等式等价于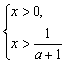 或
或![]()
即{x|x>![]() }={x|x>
}={x|x>![]() }.
}.
③若a>1时,原不等式等价于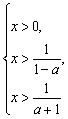 或
或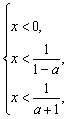
即{x|x>![]() 或x<
或x<![]() }.
}.
点评:该题还可以利用图象来解.

练习册系列答案
相关题目