题目内容
 集合M=﹛y|y=
集合M=﹛y|y= ﹜,N=﹛x|(x+1)2≤4﹜,U为全集,则图中阴影部分表示的集合是
﹜,N=﹛x|(x+1)2≤4﹜,U为全集,则图中阴影部分表示的集合是
- A.﹛x|-
 ≤x≤1﹜
≤x≤1﹜ - B.﹛x|-3≤x<0﹜
- C.﹛x|-3≤x<-
 ﹜
﹜ - D.﹛x|1<x≤
 ﹜
﹜
B
分析:通过解二次不等式求出集合M,然后利用交集、补集的定义求出中阴影部分所表示的集合.
解答:图中阴影部分所表示的集合是N∩(CUM)
∵集合M=﹛y|y= ﹜={y|0≤y≤3}
﹜={y|0≤y≤3}
∴CUM={y|y>3或y<0}
N=﹛x|(x+1)2≤4﹜={x|x2+2x-3≤0}={x|-3≤x≤1},
∴N∩(CUM)={x|-3≤x<0}
故选:B.
点评:本题考查利用集合的运算表示韦恩图中的集合、考查利用交集、补集的定义求集合的交集、补集,属于基础题.
分析:通过解二次不等式求出集合M,然后利用交集、补集的定义求出中阴影部分所表示的集合.
解答:图中阴影部分所表示的集合是N∩(CUM)
∵集合M=﹛y|y=
 ﹜={y|0≤y≤3}
﹜={y|0≤y≤3}∴CUM={y|y>3或y<0}
N=﹛x|(x+1)2≤4﹜={x|x2+2x-3≤0}={x|-3≤x≤1},
∴N∩(CUM)={x|-3≤x<0}
故选:B.
点评:本题考查利用集合的运算表示韦恩图中的集合、考查利用交集、补集的定义求集合的交集、补集,属于基础题.

练习册系列答案
相关题目
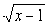 },则M∩P等于 ( )
},则M∩P等于 ( ) ,则M∩P=( )
,则M∩P=( ) },则M∩P=( )
},则M∩P=( )