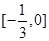题目内容
定义在R上的函数f(x)满足f(4)=1,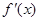 为函数f(x)的导函数,已知
为函数f(x)的导函数,已知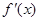 的图像如图所示,若两个正数a,b满足f (2a+b)<1,则
的图像如图所示,若两个正数a,b满足f (2a+b)<1,则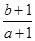 的取值范围是( )
的取值范围是( )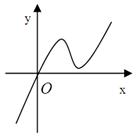
A.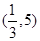 | B. | C.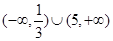 | D.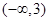 |
A
解析试题分析:由函数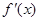 的图像可知,
的图像可知,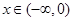 时,
时, 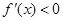 .
.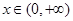 时,
时, 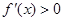 .所以函数
.所以函数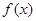 在
在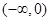 上单调递减,在
上单调递减,在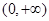 上单调递增.
上单调递增.  是两个正数,
是两个正数,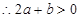 .又f(4)=1,
.又f(4)=1,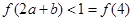 .故
.故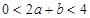 .以
.以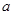 为横轴,
为横轴,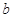 为纵轴,作出由不等式组
为纵轴,作出由不等式组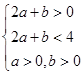 表示的平面区域.则
表示的平面区域.则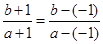 表示点
表示点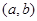 到点
到点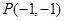 的斜率.由下图可知,点
的斜率.由下图可知,点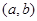 在黄色区域内,则易知
在黄色区域内,则易知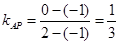 ,
,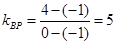 ,所以
,所以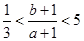 .故选A.
.故选A.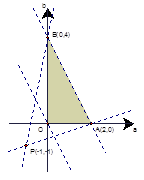
考点:线性规划、斜率公式、导函数与单调性

练习册系列答案
相关题目
下列选项中与点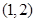 位于直线
位于直线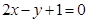 的同一侧的是( )
的同一侧的是( )
A.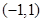 | B.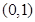 | C.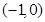 | D.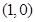 |
已知实数 满足
满足 ,则
,则 的最大值为( )
的最大值为( )
| A.11 | B.12 | C.13 | D.14 |
设实数 满足约束条件
满足约束条件 则
则 的最大值为( )
的最大值为( )
| A.-1 | B. | C.5 | D.11 |
在平面直角坐标系xoy中,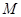 为不等式组
为不等式组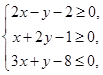 所表示的区域上一动点,则直线
所表示的区域上一动点,则直线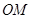 斜率的最小值为( )
斜率的最小值为( )
| A.2 | B.1 | C.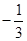 | D.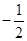 |
不等式组 表示的平面区域是( )
表示的平面区域是( )
| A.矩形 | B.三角形 | C.直角梯形 | D.等腰梯形 |
已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则z=-x+y的取值范围是( )
A.(1-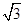 ,2) ,2) | B.(0,2) | C.(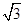 -1,2) -1,2) | D.(0,1+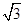 ) ) |
在圆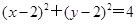 内任取一点,则该点恰好在区域
内任取一点,则该点恰好在区域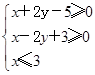 内的概率为( )
内的概率为( )
A.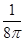 | B.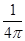 | C.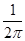 | D.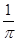 |
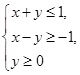 表示的平面区域为
表示的平面区域为 ,若直线
,若直线 与平面区域
与平面区域 的取值范围是( )
的取值范围是( )