题目内容
已知函数y=2sin(2x+ )(|
)(| |<
|<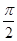 )的图象经过点(0,1),则该函数的一条对称轴方程为
)的图象经过点(0,1),则该函数的一条对称轴方程为
A.x= | B.x= | C.x=- | D.x=- |
A
解析试题分析:点在线上,点的坐标适合方程,求出φ,然后确定函数取得最大值的x值就是对称轴方程,找出选项即可.解:把(0,1)代入函数表达式,知sinφ= 因为|φ|<
因为|φ|<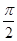 所以φ=
所以φ= ,当2x+
,当2x+ =
=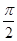 +2kπ(k∈Z)时函数取得最大值,解得对称轴方程x=
+2kπ(k∈Z)时函数取得最大值,解得对称轴方程x= +kπ(k∈Z)令k=0得x=
+kπ(k∈Z)令k=0得x= 故选A
故选A
考点:正弦函数的对称性
点评:本题考查正弦函数的对称性,考查计算能力,是基础题.取得最值的x值都是正弦函数的对称轴.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设 ,则
,则
A. | B. | C. | D. |
函数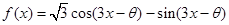 是奇函数,则
是奇函数,则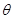 等于
等于
A. | B.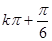 | C.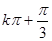 | D. |
sin(- p)= ( )
p)= ( )
A. | B.? | C.? | D. |
 ( )
( )
A. | B. | C. | D. |
如图所示,是函数y=Asin(ωx+φ)(A>0,ω>0, -p<φ<0)的简图,则振幅、周期、初相分别是 ( )
A.2, ,? ,? | B.2, ,? ,? |
C.4, ,? ,? | D.2, ,? ,? |
sin600°的值是( )
A. | B. | C. | D. |
已知角 终边上一点
终边上一点 ,则
,则 ( )
( )
A. | B. | C. | D. |
 -2x)的单调增区间是[
-2x)的单调增区间是[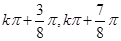 ],kÎZ
],kÎZ
 sin(wx)的最小正周期为4p,则w=
sin(wx)的最小正周期为4p,则w=