��Ŀ����
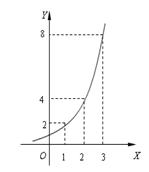
��ͼ��ʾ����ij�����еĸ�Ƽ���ӵ������m2����ʱ��x���£��Ĺ�ϵ��y=ax��������������
�����ָ�������ĵ�����2��
�ڵ�5���µĸ�Ƽ������ͻᳬ��30m2��
�۸�Ƽ��4m2���ӵ�12m2��Ҫ����1.5���£�
�ܸ�Ƽÿ�������ӵ��������ȣ�
������Ƽ���ӵ�2m2��3m2��6m2��������ʱ��ֱ�Ϊx1��x2��x3����x1+x2=x3��
������ȷ���ǣ�������

�����ָ�������ĵ�����2��
�ڵ�5���µĸ�Ƽ������ͻᳬ��30m2��
�۸�Ƽ��4m2���ӵ�12m2��Ҫ����1.5���£�
�ܸ�Ƽÿ�������ӵ��������ȣ�
������Ƽ���ӵ�2m2��3m2��6m2��������ʱ��ֱ�Ϊx1��x2��x3����x1+x2=x3��
������ȷ���ǣ�������
| A���٢� | B���٢ڢ� | C���٢ڢۢ� | D���ڢۢܢ� |

�ߵ㣨1��2���ں���ͼ���ϣ�
��2=a1��a=2���ʢ���ȷ��
�ຯ��y=2t��R�������������ҵ�t=5ʱ��y=32�ʢ���ȷ��
4��Ӧ��t=2������1.5�º������23.5��12���ʢ۲���ȷ��
��ͼ��ʾ��1-2������2m2��2-3������4m2���ʢܲ���ȷ��
�Ԣ����ڣ�2=2 x1��3=2 x 2��6=2 x3��
��x1=1��x2=log23��x3=log26��
����Ϊ1+log23=log22+log23=log22��3=log26��
������Ƽ���ӵ�2m2��3m2��6m2��������ʱ��ֱ�Ϊx1��x2��x3����x1+x2=x3������
�ʴ�Ϊ���٢ڢݣ�
��2=a1��a=2���ʢ���ȷ��
�ຯ��y=2t��R�������������ҵ�t=5ʱ��y=32�ʢ���ȷ��
4��Ӧ��t=2������1.5�º������23.5��12���ʢ۲���ȷ��
��ͼ��ʾ��1-2������2m2��2-3������4m2���ʢܲ���ȷ��
�Ԣ����ڣ�2=2 x1��3=2 x 2��6=2 x3��
��x1=1��x2=log23��x3=log26��
����Ϊ1+log23=log22+log23=log22��3=log26��
������Ƽ���ӵ�2m2��3m2��6m2��������ʱ��ֱ�Ϊx1��x2��x3����x1+x2=x3������
�ʴ�Ϊ���٢ڢݣ�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
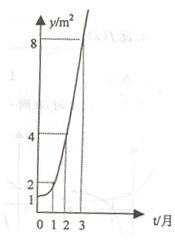 ��ͼ��ʾ����ij�����еĸ�Ƽ���ӵ������m2����ʱ�䣨�£��Ĺ�ϵ��y=ax��a��0��a��1����������������
��ͼ��ʾ����ij�����еĸ�Ƽ���ӵ������m2����ʱ�䣨�£��Ĺ�ϵ��y=ax��a��0��a��1���������������� 10����ͼ��ʾ����ij�����еĸ�Ƽ���ӵ������m2����ʱ��t���£��Ĺ�ϵ��y=at��������������
10����ͼ��ʾ����ij�����еĸ�Ƽ���ӵ������m2����ʱ��t���£��Ĺ�ϵ��y=at��������������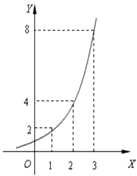 ��ͼ��ʾ����ij�����еĸ�Ƽ���ӵ������m2����ʱ��x���£��Ĺ�ϵ��y=ax��������������
��ͼ��ʾ����ij�����еĸ�Ƽ���ӵ������m2����ʱ��x���£��Ĺ�ϵ��y=ax��������������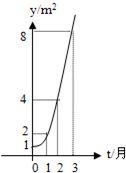 20����ͼ��ʾ����ij�����еĸ�Ƽ���ӵ����y��m2����ʱ��t���£��Ĺ�ϵ��y=at�������������⣺
20����ͼ��ʾ����ij�����еĸ�Ƽ���ӵ����y��m2����ʱ��t���£��Ĺ�ϵ��y=at�������������⣺ ��ʱ��
��ʱ�� ���£��Ĺ�ϵ��
���£��Ĺ�ϵ�� ���������������� ���ָ�������ĵ�����2���ڵ�5���µĸ�Ƽ������ͻᳬ��
���������������� ���ָ�������ĵ�����2���ڵ�5���µĸ�Ƽ������ͻᳬ�� ���۸�Ƽ��
���۸�Ƽ��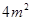 ���ӵ�
���ӵ� ��Ҫ����1.5���£��ܸ�Ƽÿ�������ӵ��������ȣ�������Ƽ���ӵ�
��Ҫ����1.5���£��ܸ�Ƽÿ�������ӵ��������ȣ�������Ƽ���ӵ� ��
�� ��
�� ��������ʱ��ֱ�Ϊ
��������ʱ��ֱ�Ϊ ����
���� .������ȷ����( )
.������ȷ����( )