题目内容
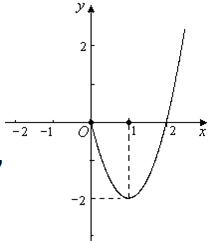若函数f（x）为奇函数，当x≥0时，f（x）=2x2-4x（如图）．（1）求函数f（x）的表达式，并补齐函数f（x）的图象；
（2）用定义证明：函数y=f（x）在区间[1，+∞）上单调递增．
分析：（Ⅰ） 任取x∈（-∞，0），则-x∈（0，+∞），由f（x）为奇函数和已知条件，求得f（x）=-f（x）的解析式，从而得到在R上的解析式，作出函数图象．
（Ⅱ）任取1≤x1＜x2，证得f（x1）-f（x2）=（2x12-4x1）-（2x22-4x2）＜0，即f（x1）＜f（x2），可得函数 y=f（x）在区间[1，+∞）上单调递增．
（Ⅱ）任取1≤x1＜x2，证得f（x1）-f（x2）=（2x12-4x1）-（2x22-4x2）＜0，即f（x1）＜f（x2），可得函数 y=f（x）在区间[1，+∞）上单调递增．
解答：
解：（Ⅰ） 任取x∈（-∞，0），则-x∈（0，+∞），
由f（x）为奇函数，
则f（x）=-f（x）=-[2（-x）2-4（-x）]=-2x2-4x．…（1分）
综上所述，f（x）=
．…（2分）
如图所示：（4分）
（Ⅱ）任取1≤x1＜x2，…（5分）
则f（x1）-f（x2）=（2x12-4x1）-（2x22-4x2） …（6分）
=2（x12-x22）-4（x1-x2）=2（x1-x2）[（x1+x2）-2]．…（7分）
∵x1＜x2，∴x1-x2＜0，x1+x2 ＞2，∴（x1+x2）-2＞0，
∴2（x1-x2）[（x1+x2）-2]＜0，∴f（x1）-f（x2）＜0，即 f（x1）＜f（x2），
∴函数 y=f（x）在区间[1，+∞）上单调递增．…（8分）
解：（Ⅰ） 任取x∈（-∞，0），则-x∈（0，+∞），由f（x）为奇函数，
则f（x）=-f（x）=-[2（-x）2-4（-x）]=-2x2-4x．…（1分）
综上所述，f（x）=
|
如图所示：（4分）
（Ⅱ）任取1≤x1＜x2，…（5分）
则f（x1）-f（x2）=（2x12-4x1）-（2x22-4x2） …（6分）
=2（x12-x22）-4（x1-x2）=2（x1-x2）[（x1+x2）-2]．…（7分）
∵x1＜x2，∴x1-x2＜0，x1+x2 ＞2，∴（x1+x2）-2＞0，
∴2（x1-x2）[（x1+x2）-2]＜0，∴f（x1）-f（x2）＜0，即 f（x1）＜f（x2），
∴函数 y=f（x）在区间[1，+∞）上单调递增．…（8分）
点评：本题主要考查函数的奇偶性和单调性的判断和证明，作函数的图象，属于中档题．
练习册系列答案
相关题目