题目内容
5.已知x,y满足不等式$\left\{\begin{array}{l}3x+2y-6≤0\\ 2x-y+2≥0\\ x-y-3≤0\end{array}\right.$,则x+y的最大值是( )| A. | $\frac{20}{7}$ | B. | $\frac{18}{7}$ | C. | $\frac{16}{7}$ | D. | $\frac{2}{7}$ |
分析 作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z=x+y的最大值.
解答 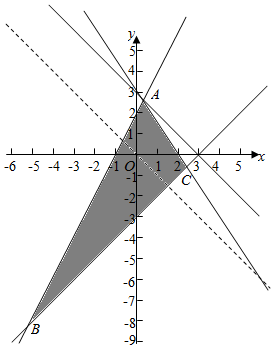 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).
设z=x+y得y=-x+z,
平移直线y=-x+z,
由图象可知当直线y=-x+z经过点A时,直线y=-x+z的截距最大,
此时z最大.
由$\left\{\begin{array}{l}{3x+2y-6=0}\\{2x-y+2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{2}{7}}\\{y=\frac{18}{7}}\end{array}\right.$,即A($\frac{2}{7}$,$\frac{18}{7}$),
代入目标函数z=x+y得z=$\frac{2}{7}$+$\frac{18}{7}$=$\frac{20}{7}$.
即目标函数z=x+y的最大值为$\frac{20}{7}$
故选:A
点评 本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.利用平移确定目标函数取得最优解的条件是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.函数f(x)=log2x•log22x取得最小值时x的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
17.四个人围坐在一张圆桌旁,每个人面前放着完全相同的硬币,所有人同时翻转自己的硬币.若硬币正面朝上,则这个人站起来; 若硬币正面朝下,则这个人继续坐着.那么,没有相邻的两个人站起来的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{16}$ | C. | $\frac{7}{16}$ | D. | $\frac{11}{16}$ |