题目内容
从空间中一点P引三条射线PA,PB,PC,且三条射线两两成60°角,则二面角A-PB-C的平面角的余弦值是( )A.

B.

C.
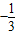
D.
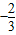
【答案】分析:在射线PB上取一点M,过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C,连接AC在△ACM中,作AN垂直于CM于点N,∠AMN就是二面角A-PB-C的平面角,解三角形AMN,即可得到二面角A-PB-C的余弦.
解答:解:在射线PB上取一点M,过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C,
所以∠AMC就是二面角A-PB-C的平面角,连接AC,
由图可得,在直角△PAM中,∠APM=60°,令PM=a,则AP=2a,AM=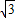 a,
a,
同理,在直角△PCM中,∠CPM=60°,令PM=a,则CP=2a CM=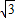 a
a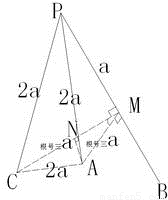 .
.
因为∠APC=60°,PA=PC=2a,
所以△PAC为等边三角形,即AC=2a.
在△ACM中,作AN垂直于CM于点N,
令MN=b,CN=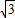 a-b,AN=x,
a-b,AN=x,
由勾股定理可得,在△AMN中有:(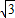 a)2-x2=b2;
a)2-x2=b2;
在△ACN中有:(2a)2-x2=( a-b)2,
a-b)2,
联合两式消去x整理的,a=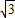 b,即
b,即  =
=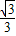 ,
,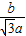 =
= ,
,
所以二面角A-PB-C的余弦值是 .
.
故选A.
点评:本题考查的知识点是二面角的平面角及求法,其中作出二面角的平面角是解答本题的关键.
解答:解:在射线PB上取一点M,过M作MA、MC垂直于PB分别相交射线PA、PC于点A、C,
所以∠AMC就是二面角A-PB-C的平面角,连接AC,
由图可得,在直角△PAM中,∠APM=60°,令PM=a,则AP=2a,AM=
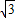 a,
a,同理,在直角△PCM中,∠CPM=60°,令PM=a,则CP=2a CM=
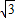 a
a .
.因为∠APC=60°,PA=PC=2a,
所以△PAC为等边三角形,即AC=2a.
在△ACM中,作AN垂直于CM于点N,
令MN=b,CN=
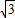 a-b,AN=x,
a-b,AN=x,由勾股定理可得,在△AMN中有:(
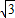 a)2-x2=b2;
a)2-x2=b2;在△ACN中有:(2a)2-x2=(
 a-b)2,
a-b)2,联合两式消去x整理的,a=
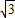 b,即
b,即  =
=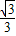 ,
,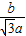 =
= ,
,所以二面角A-PB-C的余弦值是
 .
.故选A.
点评:本题考查的知识点是二面角的平面角及求法,其中作出二面角的平面角是解答本题的关键.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
从空间中一点P引三条射线PA,PB,PC,且三条射线两两成60°角,则二面角A-PB-C的平面角的余弦值是( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|