题目内容
 三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.
三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.(Ⅰ)证明平面GFE∥平面PCB;
(Ⅱ)求二面角B-AP-C的大小;
(Ⅲ)求直线PF与平面PAB所成角的大小.
分析:(Ⅰ)证明平面GFE∥平面PCB,只需证明EF∥平面PCB,GF∥平面PCB即可;
(Ⅱ)求二面角B-AP-C的大小,利用三垂线定理,作出二面角的平面角,解三角形即可.
(Ⅲ)求直线PF与平面PAB所成角的大小,设PB的中点为K,连接KC,AK,∠MPF是直线PF与平面PAB所成的角.解答即可.
或者建立空间直角坐标系,利用向量数量积求解即可.
(Ⅱ)求二面角B-AP-C的大小,利用三垂线定理,作出二面角的平面角,解三角形即可.
(Ⅲ)求直线PF与平面PAB所成角的大小,设PB的中点为K,连接KC,AK,∠MPF是直线PF与平面PAB所成的角.解答即可.
或者建立空间直角坐标系,利用向量数量积求解即可.
解答:解:方法1:
(Ⅰ)证明:因为E、F、G分别是AB、AC、AP的中点,
所以EF∥BC,GF∥CP.(1分)
因为EF、GF?平面PCB,
所以EF∥平面PCB,GF∥平面PCB.
又EF∩GF=F,
所以平面GFE∥平面PCB.(3分)
 (Ⅱ)解:过点C在平面PAC内作CH⊥PA,垂足为H.
(Ⅱ)解:过点C在平面PAC内作CH⊥PA,垂足为H.
连接HB.
因为BC⊥PC,BC⊥AC,且PC∩AC=C,
所以BC⊥平面PAC.
所以HB⊥PA.
所以∠BHC是二面角B-AP-C的平面角.(6分)
依条件容易求出CH=
.
所以tan∠BHC=
=
.
所以∠BHC=arctan
.
所以二面角B-AP-C的大小是arctan
.(8分)
 (Ⅲ)解法1:如图,设PB的中点为K,
(Ⅲ)解法1:如图,设PB的中点为K,
连接KC,AK,因为△PCB为等腰直角三角形,
所以KC⊥PB.
又AC⊥PC,AC⊥BC,且PC∩BC=C,
所以AC⊥平面PCB.
所以AK⊥PB.
因为AK∩KC=K,
所以PB⊥平面AKC.
又PB?平面PAB,
所以平面AKC⊥平面PAB.
在平面AKC内,过点F作FM⊥AK,垂足为M.
因为平面AKC⊥平面PAB,
所以FM⊥平面PAB.
连接PM,
所以∠MPF是直线PF与平面PAB所成的角.(11分)
容易求出PF=
,FM=
.
所以sin∠MPF=
=
.
所以∠MPF=arcsin
.
即直线PF与平面PAB所成的角的大小是arcsin
.(13分)
 (Ⅲ)解法2:连接FB,
(Ⅲ)解法2:连接FB,
因为PC⊥BC,PC⊥AC,且BC∩AC=C,
所以PC⊥平面ABC.
即PC是三棱锥P-ABF的高.
依条件知VP-ABF=
×PC×(
×AF×BC)
=
×1×(
×1×1)=
.
又VF-PAB=
×h×S△PAB(其中h是点F到平面PAB的距离)
=
×h×(
×
×
)=
×h×
=
h,
所以由
=
h解得h=
.(11分)
设PF与平面PAB所成的角为α,
又PF=
,
所以sinα=
=
=
.
所以α=arcsin
.
即直线AC与平面PAB所成角大小是arcsin
.(13分)
 方法2:依条件建立如图所示空间直角坐标系C-xyz.
方法2:依条件建立如图所示空间直角坐标系C-xyz.
所以A(2,0,0),B(0,1,0),P(0,0,1)
(Ⅰ)略(3分)
(Ⅱ)解:显然
=(0,1,0)是平面PAC的一
个法向量.
设n=(x,y,z)是平面PAB的一个法向量,
因为
=(-2,0,1),
=(-2,1,0),
所以由n•
=0,n•
=0解得n=(1,2,2).(6分)
设二面角B-AP-C的大小为θ,
所以cosθ=
=
.
所以二面角B-AP-C的大小为arccos
.(arccos
=arctan
)(8分)
(Ⅲ)解:设PF与平面PAB所成的角为α,
由(Ⅱ)知平面PAB的一个法向量n=(1,2,2).
又
=(-1,0,1),
所以cos(
-α)=
=
.(11分)
所以sinα=
.
所以α=arcsin
.
即直线AC与平面PAB所成角的大小是arcsin
.(13分)
(Ⅰ)证明:因为E、F、G分别是AB、AC、AP的中点,
所以EF∥BC,GF∥CP.(1分)
因为EF、GF?平面PCB,
所以EF∥平面PCB,GF∥平面PCB.
又EF∩GF=F,
所以平面GFE∥平面PCB.(3分)
 (Ⅱ)解:过点C在平面PAC内作CH⊥PA,垂足为H.
(Ⅱ)解:过点C在平面PAC内作CH⊥PA,垂足为H.连接HB.
因为BC⊥PC,BC⊥AC,且PC∩AC=C,
所以BC⊥平面PAC.
所以HB⊥PA.
所以∠BHC是二面角B-AP-C的平面角.(6分)
依条件容易求出CH=
| 2 | ||
|
所以tan∠BHC=
| 1 | ||||
|
| ||
| 2 |
所以∠BHC=arctan
| ||
| 2 |
所以二面角B-AP-C的大小是arctan
| ||
| 2 |
 (Ⅲ)解法1:如图,设PB的中点为K,
(Ⅲ)解法1:如图,设PB的中点为K,连接KC,AK,因为△PCB为等腰直角三角形,
所以KC⊥PB.
又AC⊥PC,AC⊥BC,且PC∩BC=C,
所以AC⊥平面PCB.
所以AK⊥PB.
因为AK∩KC=K,
所以PB⊥平面AKC.
又PB?平面PAB,
所以平面AKC⊥平面PAB.
在平面AKC内,过点F作FM⊥AK,垂足为M.
因为平面AKC⊥平面PAB,
所以FM⊥平面PAB.
连接PM,
所以∠MPF是直线PF与平面PAB所成的角.(11分)
容易求出PF=
| 2 |
| 1 |
| 3 |
所以sin∠MPF=
| ||
|
| ||
| 6 |
所以∠MPF=arcsin
| ||
| 6 |
即直线PF与平面PAB所成的角的大小是arcsin
| ||
| 6 |
 (Ⅲ)解法2:连接FB,
(Ⅲ)解法2:连接FB,因为PC⊥BC,PC⊥AC,且BC∩AC=C,
所以PC⊥平面ABC.
即PC是三棱锥P-ABF的高.
依条件知VP-ABF=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
又VF-PAB=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 | ||
|
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
所以由
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
设PF与平面PAB所成的角为α,
又PF=
| 2 |
所以sinα=
| h |
| PF |
| ||
|
| ||
| 6 |
所以α=arcsin
| ||
| 6 |
即直线AC与平面PAB所成角大小是arcsin
| ||
| 6 |
 方法2:依条件建立如图所示空间直角坐标系C-xyz.
方法2:依条件建立如图所示空间直角坐标系C-xyz.所以A(2,0,0),B(0,1,0),P(0,0,1)
(Ⅰ)略(3分)
(Ⅱ)解:显然
| CB |
个法向量.
设n=(x,y,z)是平面PAB的一个法向量,
因为
| AP |
| AB |
所以由n•
| AP |
| AB |
设二面角B-AP-C的大小为θ,
所以cosθ=
| ||
|
|
| 2 |
| 3 |
所以二面角B-AP-C的大小为arccos
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
(Ⅲ)解:设PF与平面PAB所成的角为α,
由(Ⅱ)知平面PAB的一个法向量n=(1,2,2).
又
| FP |
所以cos(
| π |
| 2 |
| ||
|
|
| ||
| 6 |
所以sinα=
| ||
| 6 |
所以α=arcsin
| ||
| 6 |
即直线AC与平面PAB所成角的大小是arcsin
| ||
| 6 |
点评:本题考查直线与平面垂直和平行的判定,直线与平面所成的角,空间向量的数量积,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.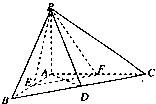 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中,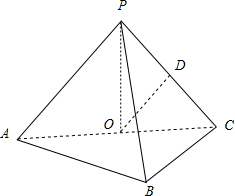 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.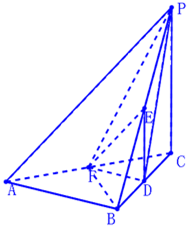 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.