题目内容
 如图,
如图,| AC |
| BC |
分析:先利用向量减法的三角形法则求得
,然后求出
、
,根据向量夹角公式即可求得两个向量夹角余弦.
| AB |
| CE |
| CF |
解答:解:
=
-
=(3,-3)-(-3,-3)=(6,0),
所以
=
-
=
-
=(2,0)-(3,3)=(-1,-3),
=
-
=
-
=(4,0)-(3,3)=(1,-3),
所以cos∠ECF=
=
=
,
故选D.
| AB |
| CB |
| CA |
所以
| CE |
| AE |
| AC |
| 1 |
| 3 |
| AB |
| AC |
| CF |
| AF |
| AC |
| 2 |
| 3 |
| AB |
| AC |
所以cos∠ECF=
| ||||
|
|
| 8 | ||||
|
| 4 |
| 5 |
故选D.
点评:本题考查向量的线性运算、数量积运算,考查向量夹角公式,属中档题.

练习册系列答案
相关题目
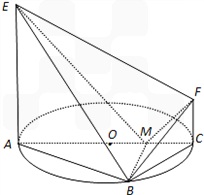
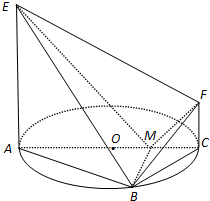 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.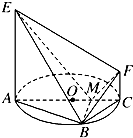 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.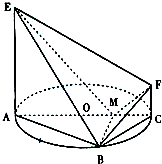 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.