题目内容
已知数列{an}的前n项和Sn满足Sn=2an+(-1)n,n≥1.(1)写出数列{an}的前三项a1,a2,a3;
(2)试判断数列
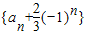 是否为等比数列,如果是,求出
是否为等比数列,如果是,求出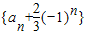 的通项公式;如果不是,请说明理由;
的通项公式;如果不是,请说明理由;(3)证明:对任意的整数m>4,有
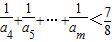 .
.
【答案】分析:(1)是考查已知递推公式求前几项,属于基础题,需注意的是S1=a1,需要先求出a1才能求出a2,这是递推公式的特点.
(2)由已知化简得,an=2an-1+2(-1)n-1,进而可变为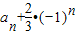 =2[an-1+
=2[an-1+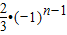 ],利用等比数列的定义可作出判断;
],利用等比数列的定义可作出判断;
(3)的解答需要在代换后,适当的变形,利用不等式放缩法进行放缩.
解答:解:(1)当n=1时,有:S1=a1=2a1+(-1)⇒a1=1;
当n=2时,有:S2=a1+a2=2a2+(-1)2⇒a2=0;
当n=3时,有:S3=a1+a2+a3=2a3+(-1)3⇒a3=2;
综上可知a1=1,a2=0,a3=2;
(2)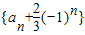 是等比数列,理由如下:
是等比数列,理由如下:
由已知得:an=Sn-Sn-1=2an+(-1)n-2an-1-(-1)n-1
化简得:an=2an-1+2(-1)n-1
上式可化为: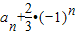 =2[an-1+
=2[an-1+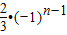 ]
]
故数列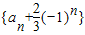 是以
是以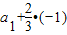 1=
1= 为首项,公比为2的等比数列.
为首项,公比为2的等比数列.
(3)由(2)可知: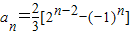 ,
,
所以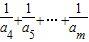 =
= [
[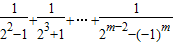 ]
]
= [
[ +
+ +
+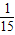
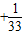 +
+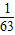 +…+
+…+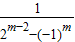 ]
]
= [1+
[1+ +
+ +
+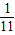 +
+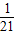 +…]
+…]
< (1+
(1+ +
+ +
+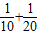 +…)
+…)
= [
[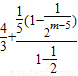 ]=
]= [
[ +
+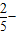
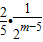 ]
]
=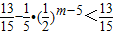 =
=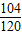 <
<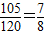 .
.
点评:本题考查的递推数列较为典型,对数列有关公式的应用是高考考查的重点,要能熟练的应用.(3)中不等式证明中的放缩是一个难点,需要有扎实的基本功及一定的运算能力,对运算放缩能力要求较高.
(2)由已知化简得,an=2an-1+2(-1)n-1,进而可变为
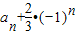 =2[an-1+
=2[an-1+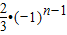 ],利用等比数列的定义可作出判断;
],利用等比数列的定义可作出判断;(3)的解答需要在代换后,适当的变形,利用不等式放缩法进行放缩.
解答:解:(1)当n=1时,有:S1=a1=2a1+(-1)⇒a1=1;
当n=2时,有:S2=a1+a2=2a2+(-1)2⇒a2=0;
当n=3时,有:S3=a1+a2+a3=2a3+(-1)3⇒a3=2;
综上可知a1=1,a2=0,a3=2;
(2)
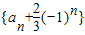 是等比数列,理由如下:
是等比数列,理由如下:由已知得:an=Sn-Sn-1=2an+(-1)n-2an-1-(-1)n-1
化简得:an=2an-1+2(-1)n-1
上式可化为:
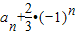 =2[an-1+
=2[an-1+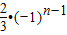 ]
]故数列
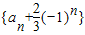 是以
是以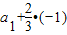 1=
1= 为首项,公比为2的等比数列.
为首项,公比为2的等比数列.(3)由(2)可知:
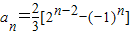 ,
,所以
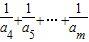 =
= [
[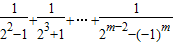 ]
]=
 [
[ +
+ +
+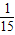
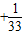 +
+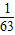 +…+
+…+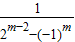 ]
]=
 [1+
[1+ +
+ +
+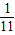 +
+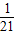 +…]
+…]<
 (1+
(1+ +
+ +
+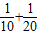 +…)
+…)=
 [
[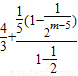 ]=
]= [
[ +
+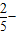
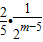 ]
]=
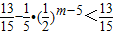 =
=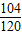 <
<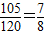 .
.点评:本题考查的递推数列较为典型,对数列有关公式的应用是高考考查的重点,要能熟练的应用.(3)中不等式证明中的放缩是一个难点,需要有扎实的基本功及一定的运算能力,对运算放缩能力要求较高.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |