题目内容
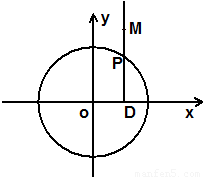
如图所示,点P在圆O:x2+y2=4上,PD⊥x轴,点M在射线DP上,且满足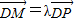 (λ≠0).
(λ≠0).(Ⅰ)当点P在圆O上运动时,求点M的轨迹C的方程,并根据λ取值说明轨迹C的形状.
(Ⅱ)设轨迹C与x轴正半轴交于点A,与y轴正半轴交于点B,直线2x-3y=0与轨迹C交于点E、F,点G在直线AB上,满足
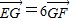 ,求实数λ的值.
,求实数λ的值.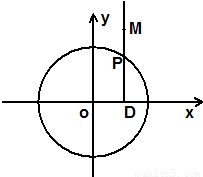
【答案】分析:(Ⅰ)利用 和PD⊥x轴,确定M,P坐标之间的关系,代入圆方程得:
和PD⊥x轴,确定M,P坐标之间的关系,代入圆方程得: ,对λ讨论,即可得到结论;
,对λ讨论,即可得到结论;
(Ⅱ)由题设知A(2,0),B(0,2λ),E,F关于原点对称,可设E,F,G的坐标,利用 ,即可求得结论.
,即可求得结论.
解答:解:(Ⅰ)设M(x,y)、P(x,y),由于 和PD⊥x轴,所以
和PD⊥x轴,所以 ,∴
,∴
代入圆方程得: --------------(2分)
--------------(2分)
当0<λ<1时,轨迹C表示焦点在x轴上的椭圆;
当λ=1时轨迹C就是圆O;
当λ>1时轨迹C表示焦点是y轴上的椭圆.---------------(4分)
(Ⅱ)由题设知A(2,0),B(0,2λ),E,F关于原点对称,所以设 ,
, ,G(x,y),不妨设x1>0---------------(6分)
,G(x,y),不妨设x1>0---------------(6分)
直线AB的方程为: ,把点G坐标代入得y=2λ-λx
,把点G坐标代入得y=2λ-λx
又点E在轨迹C上,则有 ,∴
,∴ -------(8分)
-------(8分)
∵ ,∴x-x1=6(-x1-x),∴
,∴x-x1=6(-x1-x),∴
∵y- x1=6(-
x1=6(- x1-y),∴
x1-y),∴ ----------(10分)
----------(10分)
∴ =
= (λ>0),∴18λ2+50λ-17=0,∴
(λ>0),∴18λ2+50λ-17=0,∴ ---------(12分)
---------(12分)
点评:本题考查轨迹方程,考查向量知识的运用,利用向量确定坐标之间的关系是关键.
 和PD⊥x轴,确定M,P坐标之间的关系,代入圆方程得:
和PD⊥x轴,确定M,P坐标之间的关系,代入圆方程得: ,对λ讨论,即可得到结论;
,对λ讨论,即可得到结论;(Ⅱ)由题设知A(2,0),B(0,2λ),E,F关于原点对称,可设E,F,G的坐标,利用
 ,即可求得结论.
,即可求得结论.解答:解:(Ⅰ)设M(x,y)、P(x,y),由于
 和PD⊥x轴,所以
和PD⊥x轴,所以 ,∴
,∴
代入圆方程得:
 --------------(2分)
--------------(2分)当0<λ<1时,轨迹C表示焦点在x轴上的椭圆;
当λ=1时轨迹C就是圆O;
当λ>1时轨迹C表示焦点是y轴上的椭圆.---------------(4分)
(Ⅱ)由题设知A(2,0),B(0,2λ),E,F关于原点对称,所以设
 ,
, ,G(x,y),不妨设x1>0---------------(6分)
,G(x,y),不妨设x1>0---------------(6分)直线AB的方程为:
 ,把点G坐标代入得y=2λ-λx
,把点G坐标代入得y=2λ-λx又点E在轨迹C上,则有
 ,∴
,∴ -------(8分)
-------(8分)∵
 ,∴x-x1=6(-x1-x),∴
,∴x-x1=6(-x1-x),∴
∵y-
 x1=6(-
x1=6(- x1-y),∴
x1-y),∴ ----------(10分)
----------(10分)∴
 =
= (λ>0),∴18λ2+50λ-17=0,∴
(λ>0),∴18λ2+50λ-17=0,∴ ---------(12分)
---------(12分)点评:本题考查轨迹方程,考查向量知识的运用,利用向量确定坐标之间的关系是关键.

练习册系列答案
相关题目
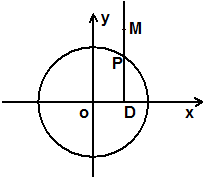 如图所示,点P在圆O:x2+y2=4上,PD⊥x轴,点M在射线DP上,且满足
如图所示,点P在圆O:x2+y2=4上,PD⊥x轴,点M在射线DP上,且满足 如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且
如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且 (λ≠0).
(λ≠0).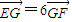 ,求实数λ的值.
,求实数λ的值.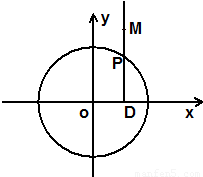
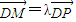 (λ≠0).
(λ≠0).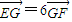 ,求实数λ的值.
,求实数λ的值.