题目内容
设命题p:函数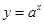 在R上单调递增,命题q:不等式
在R上单调递增,命题q:不等式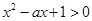 对于
对于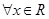 恒成立,若“
恒成立,若“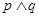 ”为假,“
”为假,“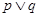 ”为真,求实数
”为真,求实数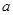 的取值范围
的取值范围

解析试题分析:∵命题p:函数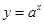 在R上单调递增,∴a>1,
在R上单调递增,∴a>1,
又命题q:不等式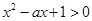 对于
对于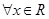 恒成立
恒成立
△=(-a) -4<0, ∴-2<a<2
-4<0, ∴-2<a<2
∵“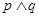 ”为假,“
”为假,“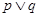 ”为真, ∴p,q必一真一假;
”为真, ∴p,q必一真一假;
(1)当p真,q假时,有 ,∴
,∴
(2) 当p假,q真时,有 ,∴-2<a≤1.
,∴-2<a≤1.
综上, 实数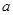 的取值范围为
的取值范围为 -------12分
-------12分
考点:本题考查了复合命题的真假
点评:“P或Q”是真命题,“P且Q”是假命题,根据真假表知,P,Q之中一真一假,因此有两种情况,要分类讨论

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
 ;命题
;命题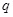 :不等式
:不等式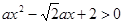 对任意
对任意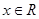 恒成立.若
恒成立.若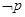 为真,且
为真,且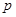 或
或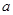 的取值范围.
的取值范围.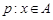 ,且
,且 ,命题
,命题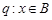 ,且
,且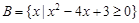 .
.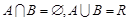 ,求实数
,求实数 的值;
的值;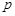 是
是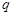 的充分条件,求实数
的充分条件,求实数 :
: ,命题
,命题 :
: ;
; 的取值范围。
的取值范围。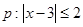 ;
;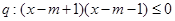 ,若
,若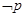 是
是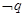 的充分而不必要条件,求实数
的充分而不必要条件,求实数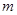 的范围.
的范围. ;
; 若
若 是
是 的必要非充分条件,求实数
的必要非充分条件,求实数 的取值范围。
的取值范围。 条件q:
条件q:  若
若 的充分但不必要条件,求实数
的充分但不必要条件,求实数 的取值范围.
的取值范围. :
: 在
在 上是增函数;命题
上是增函数;命题 函数
函数 存在极大值和极小值。求使命题“
存在极大值和极小值。求使命题“ ”为真命题的
”为真命题的 的取值范围。
的取值范围。 :对任意
:对任意 ,不等式
,不等式 恒成立;
恒成立; :存在
:存在 ,使不等式
,使不等式 成立,若“
成立,若“ 的取值范围.
的取值范围.