题目内容
求圆心在直线y=-4x上,并且与直线l:x+y-1=0相切于点P(3,-2)的圆的方程.思路分析:由于题目涉及到圆心,因此可设圆的方程为(x-a)2+(y-b)2=r2.用待定系数法来求.
充分揭示几何性质,运用分析的方法求圆心坐标与半径,从而圆的方程可求出.
解法一:设所求的圆的方程为(x-a)2+(y-b)2=r2.
依题设有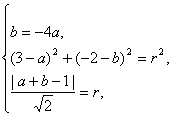 解方程组得a=1,b=-4,r=2
解方程组得a=1,b=-4,r=2![]() .
.
故所求圆的方程为(x-1)2+(y+4)2=8.
解法二:由于圆心在y=-4x上,又在过切点(3,-2)与切线x+y-1=0垂直的直线y+2=x-3,即x-y-5=0上.解方程组![]() 可得圆心(1,-4),于是r=
可得圆心(1,-4),于是r=![]() .故所求圆的方程为(x-1)2+(y+4)2=8.
.故所求圆的方程为(x-1)2+(y+4)2=8.
解法三:设圆的方程为x2+y2+Dx+Ey+F=0.
由题意,得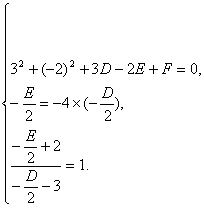
解得D=-2,E=8,F=9.
故圆的方程为x2+y2-2x+8y+9=0.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目