Question

对于函数f（x）=

sinx ，sinx≤cosx cosx ，sinx＞cosx

，给出下列四个命题：
①该函数是以π为最小正周期的周期函数；
②当且仅当x=π+kπ（k∈Z）时，该函数取得最小值-1；
③该函数的图象关于x=

5π

4

+2kπ（k∈Z）对称；
④当且仅当2kπ＜x＜

π

2

+2kπ（k∈Z）时，0＜f（x）≤

2

2

．
其中正确命题的序号是

 

．（请将所有正确命题的序号都填上）

Answer 1

分析：由题意作出此分段函数的图象，由图象研究该函数的性质，依据这些性质判断四个命题的真假，此函数取自变量相同时函数值小的那一个，由此可顺利作出函数图象．

解答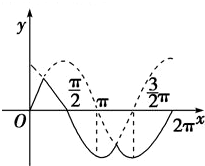：解：由题意函数f（x）=

sinx ，sinx≤cosx cosx ，sinx＞cosx

，画出f（x）在x∈[0，2π]上的图象．
由图象知，函数f（x）的最小正周期为2π，
在x=π+2kπ（k∈Z）和x=

3π

2

+2kπ（k∈Z）时，该函数都取得最小值-1，故①②错误，
由图象知，函数图象关于直线x=

5π

4

+2kπ（k∈Z）对称，
在2kπ＜x＜

π

2

+2kπ（k∈Z）时，0＜f（x）≤

2

2

，故③④正确．
故答案为   ③④

点评：本题考点是三角函数的最值，本题是函数图象的运用，由函数的图象研究函数的性质，并以由图象研究出的结论判断和函数有关的命题的真假．