题目内容
18.在△ABC中,已知a2-(b2-c2)=(2-$\sqrt{3}$)bc,sinA•sinB=cos2$\frac{C}{2}$,(1)求角A,角B;
(2)求sinB•sinC的值.
分析 (1)由条件sinA•sinB=cos2$\frac{C}{2}$求得得cos(A-B)=1,可得A=B,a=b.再根据a2-(b2-c2)=(2-$\sqrt{3}$)bc,利用余弦定理求得cosB的值,可得角A,角B的值.
(2)由(1)可得sinC=2sinAcosA,可得sinB•sinC=2sin2AcosA,化简求得结果.
解答 解:(1)△ABC中,∵sinA•sinB=cos2$\frac{C}{2}$=$\frac{1+cosC}{2}$,∴2sinA•sinB=1+cosC=1-cos(A+B)=1-cosAcosB+sinAsinB,
化简可得cos(A-B)=1,∴A-B=0,即 A=B,∴a=b.
再根据a2-(b2-c2)=(2-$\sqrt{3}$)bc,利用余弦定理可得 2ac•cosB=(2-$\sqrt{3}$)ac,∴cosB=1-$\frac{\sqrt{3}}{2}$=cosA,
∴A=B=arccos(1-$\frac{\sqrt{3}}{2}$).
(2)由以上可得,sinC=sin(A+B)=sin2A=2sinAcosA,∴sinB•sinC=2sin2AcosA=2cosA•(1-cos2A)
=( 2-$\sqrt{3}$)•($\sqrt{3}$-$\frac{3}{4}$)=$\frac{5\sqrt{3}-18}{4}$.
点评 本题主要考查正弦定理和余弦定理的应用,二倍角公式、诱导公式、以及两角和的三角公式,属于中档题.

练习册系列答案
相关题目
6.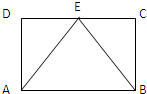 如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )
如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )
 如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )
如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
3.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 57600 | B. | 576000 | C. | 41600 | D. | 1600(22+$\sqrt{17}$) |