题目内容
如图，⊙O中弦AB，CD相交于点P，已知AP=3，BP=2，CP=1，则DP=（ ）
| A、3 | B、4 | C、5 | D、6 |
分析：根据相交弦定理“圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等”进行计算．
解答：解：由相交弦定理得：
PA•PB=PC•PD，
∴DP=
=
=6．
故选D．
PA•PB=PC•PD，
∴DP=
| PA•PB |
| PC |
| 3×2 |
| 1 |
故选D．
点评：本题主要考查相交弦定理“圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等”的应用．属于基础题．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
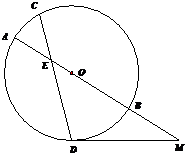如图，⊙O中的弦CD与直径AB相交于点E，M为AB延长线上一点，MD为⊙O的切线，D为切点，若AE=2，DE=4，CE=3，DM=4，则OB=
【选做题】在A，B，C，D四小题中只能选做2题，每小题10分，共计20分．请在答题卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．
（几何证明选讲选做题）如图，⊙O中的弦AB与直径CD相交于P，M为DC延长线上一点，MN为⊙O的切线，N为切点，若AP=8，PB=6，PD=4，MC=6，则MN的长为
（2013•蓟县二模）如图，⊙O中的弦AB与直径CD相交于点P，M为DC延长线上一点，MN为⊙O的切线，N为切点，若AP=2BP=4，PC=1，MN=6，则MC的长为