题目内容
19.在平面直角坐标系xOy中，已知圆心在第二象限、半径为2
的圆C与直线y=x相切于坐标原点O.椭圆
=1与圆C的一个交点到椭圆两焦点的距离之和为10.(1)求圆C的方程；
(2)试探究圆C上是否存在异于原点的点Q，使Q到椭圆右焦点F的距离等于线段OF的长.若存在，请求出点Q的坐标；若不存在，请说明理由.
解：（1）设圆C的圆心为A（p,q）,则圆C的方程为（x-p）2+(y-q)2=8,
∵直线y=x与圆C相切于坐标原点O，∴O在圆C上，且直线OA垂直于直线y=x.
于是有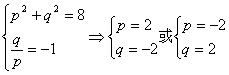
由于点A（p,q）在第二象限，故p＜0.
所以圆C的方程为（x+2）2+(y-2)2=8.
（2）∵椭圆
∴2a=10
a=5.故椭圆右焦点为F（4，0）.
若圆C上存在异于原点的点Q（x0,y0）到椭圆右焦点F的距离等于线段OF的长 ，
则有|QF|=|OF|，于是（x0-4）2+y
=42,且x
+y
≠0.(1)
由于Q（x0,y0）在圆上，故有（x0+2）2+(y0-2)2=8.(2)
解（1）和（2）得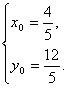
故圆C上存在满足条件的点Q（
）.
练习册系列答案
相关题目
如图，在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．若点A的横坐标是