题目内容
11.已知平面α∥平面β,异面直线a,b分别在α,β内,直线l⊥a,l⊥b,求证:l⊥α,l⊥β.分析 由题意过l与a的交点作b′∥b,过l与b的交点作a′∥a,可得b′?α,a′?β,证明直线l⊥a′,l⊥b′,利用线面垂直的判定,即可证明l⊥α,l⊥β.
解答  证明:如图,由题意过l与a的交点作b′∥b,过l与b的交点作a′∥a,
证明:如图,由题意过l与a的交点作b′∥b,过l与b的交点作a′∥a,
∵平面α∥平面β,
∴b′?α,a′?β,
∵直线l⊥a,l⊥b,
∴直线l⊥a′,l⊥b′,
∴l⊥α,l⊥β.
点评 本题线面垂直的定义,线面平行的判定,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
2.已知集合={x|1-x>0},B={x|2x>1},则A∩B=( )
| A. | ∅ | B. | {x|0<x<1} | C. | {x|x<0} | D. | {x|x>1} |
19. 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
 某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{6}$ |
16.根据如下样本数据得到的回归方程为$\stackrel{∧}{y}$=bx+a.若a=7.9,则x每增加1个单位,y就( )
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4 | 2.5 | -0.5 | 0.5 | -2 |
| A. | 增加1.4个单位 | B. | 减少1.4个单位 | C. | 增加1.2个单位 | D. | 减少1.2个单位. |
 ,
,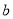 ,
,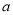 ,
, …的一个通项公式是_________.
…的一个通项公式是_________.