题目内容
已知函数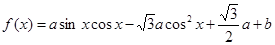
(1)当a
〉0时，写出函数的单调递减区间；
(2)设
，
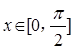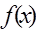的最小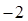值是
，最大值是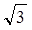
，求实数
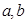的值．
【答案】
因为
，则由
则
则函数的单调递减区间为
（2）当
时，
则
①当时
则有
解得
②当时
则有
解得
【解析】将函数化成
，求减区间；（2）先求出，讨论a的正负。
练习册系列答案
相关题目
时，讨论f(x)的单调性．
(1)当a=4,
,求函数f(x)的最大值；(2)若x≥a , 试求f(x)+3 ＞0 的解集；(3)当
时，f(x)≤2x – 2 恒成立，求实数a的取值范围.
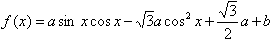
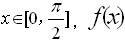的最小值是-2，最大值是
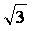，求实数
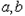的值．