题目内容
如图,在正三棱柱![]() 中,D是BC的中点,
中,D是BC的中点,![]() 。
。
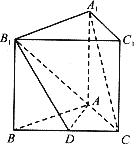
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求点C到平面![]() 的距离。
的距离。
解:(1)连接![]() ,设
,设![]() ,连接DE,如图所示。
,连接DE,如图所示。
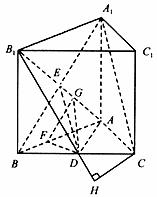
∵![]() 是正三棱柱, 且
是正三棱柱, 且![]()
∴四边形![]() 是正方形,
是正方形,
∴E是![]() 的中点,又D是BC的中点,
的中点,又D是BC的中点,
∴ ![]() ∥
∥![]() 。
。
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ∥平面
∥平面![]() 。
。
(2)在平面ABC内作DF⊥AB于点F,在平面![]() 内作FG ⊥
内作FG ⊥![]() 于点G,连接DG。
于点G,连接DG。
∵平面![]() ⊥平面ABC,
⊥平面ABC,
∴DF⊥平面![]() ,
,
∴FG是DG在平面![]() 上的射影,
上的射影,
∵FG⊥![]() ,∴ DG⊥
,∴ DG⊥![]() 。
。
∴∠FGD是二面角![]() 的平面角。
的平面角。
设![]() ,
,
在正![]() 中,
中,![]()
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
所以,二面角![]() 的大小为
的大小为![]() 。
。
(3)∵平面![]() ⊥平面ABC,且AD⊥BC,
⊥平面ABC,且AD⊥BC,
∴AD⊥平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() ⊥平面
⊥平面![]() 。
。
在平面![]() 内作CH⊥
内作CH⊥![]() 交
交![]() 的延长线于点H。
的延长线于点H。
则CH的长度就是点C到平面![]() 的距离。
的距离。
由![]() ∽
∽![]() ,得
,得![]() 。
。
即点C到平面![]() 的距离是
的距离是![]() 。
。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,在正三棱柱中,AB=2,AA1=2由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线与棱AA1的交点记为M,求:
如图,在正三棱柱中,AB=2,AA1=2由顶点B沿棱柱侧面经过棱AA1到顶点C1的最短路线与棱AA1的交点记为M,求:
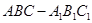 中,
中, ,
, 是
是 的中点,
的中点, 是线段
是线段 上的动点(与端点不重合),且
上的动点(与端点不重合),且 .
.
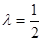 ,求证:
,求证: ;
; 与平面
与平面 所成角的大小为
所成角的大小为 ,求
,求 的最大值.
的最大值. 中,D为棱
中,D为棱 的中点,若截面
的中点,若截面 是面积为6的直角三角形,则此三棱柱的体积为
。
是面积为6的直角三角形,则此三棱柱的体积为
。
 中,
中,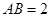 .若二面角
.若二面角 的大小为
的大小为 ,则点
,则点 到平面
到平面 的距离为
。
的距离为
。 