Question

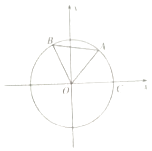
【题目】如图，点A，B是单位圆O上的两点，A，B点分别在第一，而象限，点C是圆O与x轴正半轴的交点，若∠COA=60°，∠AOB=α，点B的坐标为（﹣ ， ）．
（1）求sinα的值；
（2）已知动点P沿圆弧从C点到A点匀速运动需要2秒钟，求动点P从A点开始逆时针方向作圆周运动时，点P的纵坐标y关于时间t（秒）的函数关系式．

Answer 1

【答案】
（1）解：∵点B的坐标为（﹣ ， ），

∴sin∠COB= ，cos∠COB=﹣ ，

∴sinα=sin（∠COB﹣60°）=

（2）解：∵动点P沿圆弧从C点到A点匀速运动需要2秒钟，∠COA=60°

∴ω=

∴点P的纵坐标y关于时间t（秒）的函数关系式为y=sin（ t+ ）（t≥0）

【解析】（1）利用点B的坐标，根据三角函数的定义可知sin∠COB= ，cos∠COB=﹣ ，进而可求sinα=sin（∠COB﹣60°）= ；（2）根据动点P沿圆弧从C点到A点匀速运动至少需要2秒钟，∠COA=60°，可求ω= ，进而可求点P到x轴的距离d关于时间t的函数关系式．