题目内容
已知函数f(x)=a1x+a2x2+a3x3+…+anxn(n∈N*)且a1,a2,…,an构成一个数列,又f(1)=n2
(1)求数列{an} 的通项公式;
(2)比较f( )与1的大小.
)与1的大小.
解:(1)f(1)=n2
得出a1+a2+a3+…+an=n2 ①
当n≥2时a1+a2+a3+…+an-1=(n-1)2 ②
①-②得an=n2-(n-1)2=2n-1
又在①中令n=1得出a1=1,也适合上式
所以数列{an} 的通项公式an=2n-1.
(2)f( )=(
)=( )+3(
)+3( )2+5(
)2+5( )3+…+(2n-1)(
)3+…+(2n-1)( )n,
)n,
两边都乘以 ,可得
,可得 f(
f( )=(
)=( )2+3(
)2+3( )3+5(
)3+5( )4+…+(2n-1)(
)4+…+(2n-1)( )n+1,
)n+1,
两式相减,得 f(
f( )=(
)=( )+2(
)+2( )2+2(
)2+2( )3+…+2(
)3+…+2( )n…-(2n-1)(
)n…-(2n-1)( )n+1,
)n+1,
= +
+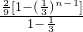 -(2n-1)(
-(2n-1)( )n+1,
)n+1,
=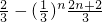
则f( )=
)= <1
<1
分析:(1)f(1)=n2,得出a1+a2+a3+…+an=n2,当n≥2时a1+a2+a3+…+an-1=(n-1)2,两式相减求通项即可.
(2)由(1)应得出f( )=(
)=( )+3(
)+3( )2+5(
)2+5( )3+…+(2n-1)(
)3+…+(2n-1)( )n,将f(
)n,将f( )看成一个数列的前n项和,由错位相减法求出,再与1比较.
)看成一个数列的前n项和,由错位相减法求出,再与1比较.
点评:本题考查数列与函数的综合,涉及等差数列的性质与错位相减法求数列的前n项和;考查构造、变形、计算、推理论证能力.
得出a1+a2+a3+…+an=n2 ①
当n≥2时a1+a2+a3+…+an-1=(n-1)2 ②
①-②得an=n2-(n-1)2=2n-1
又在①中令n=1得出a1=1,也适合上式
所以数列{an} 的通项公式an=2n-1.
(2)f(
 )=(
)=( )+3(
)+3( )2+5(
)2+5( )3+…+(2n-1)(
)3+…+(2n-1)( )n,
)n,两边都乘以
 ,可得
,可得 f(
f( )=(
)=( )2+3(
)2+3( )3+5(
)3+5( )4+…+(2n-1)(
)4+…+(2n-1)( )n+1,
)n+1,两式相减,得
 f(
f( )=(
)=( )+2(
)+2( )2+2(
)2+2( )3+…+2(
)3+…+2( )n…-(2n-1)(
)n…-(2n-1)( )n+1,
)n+1,=
 +
+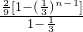 -(2n-1)(
-(2n-1)( )n+1,
)n+1,=
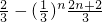
则f(
 )=
)= <1
<1分析:(1)f(1)=n2,得出a1+a2+a3+…+an=n2,当n≥2时a1+a2+a3+…+an-1=(n-1)2,两式相减求通项即可.
(2)由(1)应得出f(
 )=(
)=( )+3(
)+3( )2+5(
)2+5( )3+…+(2n-1)(
)3+…+(2n-1)( )n,将f(
)n,将f( )看成一个数列的前n项和,由错位相减法求出,再与1比较.
)看成一个数列的前n项和,由错位相减法求出,再与1比较.点评:本题考查数列与函数的综合,涉及等差数列的性质与错位相减法求数列的前n项和;考查构造、变形、计算、推理论证能力.

练习册系列答案
相关题目