题目内容
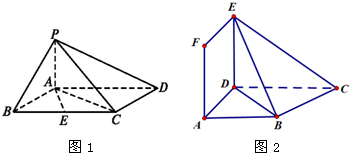
如图1是正方形ABCD与顶角为120 °的等腰△ABE组成的一个平面图形,其中AE=AB=4,翻折正方形所在平面ABCD使得与平面AEB垂直(如图2),F为线段EA的中点.
(1)若H是线段BD上的中点,求证:FH // 平面CDE;
(2)若H是线段BD上的一个动点,设直线FH与平面ABCD所成角的大小为θ,求tanθ的最小值.
(1)若H是线段BD上的中点,求证:FH // 平面CDE;
(2)若H是线段BD上的一个动点,设直线FH与平面ABCD所成角的大小为θ,求tanθ的最小值.

证明: (1)连结AC,H是线段AC的中点,
又F为线段EA的中点,
所以FH // CE,
又FH不在平面CDE内,CE 平面CDE,
平面CDE,
所以FH // 平面CDE.
(2)在平面ABE内,过F作AB的垂线交AB于M,连结MH,
平面ABCD⊥平面AEB,FM⊥AB,
所以FM⊥平面ABCD,
∠FHM就是直线FH与平面ABCD所成的角θ, ;
;
过H作AB的垂线交AB于N,设 ,
, ,
,
则 ,
, ,
, ,
,
所以

当 时,
时, 取得最大值
取得最大值 ,
, 有最小值,
有最小值,
又 , 得
, 得 .
.
所以tanθ的最小值是 .
.
又F为线段EA的中点,
所以FH // CE,
又FH不在平面CDE内,CE
 平面CDE,
平面CDE,所以FH // 平面CDE.
(2)在平面ABE内,过F作AB的垂线交AB于M,连结MH,
平面ABCD⊥平面AEB,FM⊥AB,
所以FM⊥平面ABCD,
∠FHM就是直线FH与平面ABCD所成的角θ,
 ;
;过H作AB的垂线交AB于N,设
 ,
, ,
,则
 ,
, ,
, ,
,所以


当
 时,
时, 取得最大值
取得最大值 ,
, 有最小值,
有最小值,又
 , 得
, 得 .
.所以tanθ的最小值是
 .
.
练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC, BC.
BC. BC.
BC.