Question

（本小题满分12分）如图，多面体ABCDS中，面ABCD为矩形， ，

   （1）求证：CD;   （2）求AD与SB所成角的余弦值;

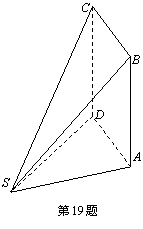   （3）求二面角A—SB—D的余弦值．

 

 

 

 

 

 

 

 

 

 

 

 

 

 

_{高☆考♂资♀源*网}

Answer 1

解：（I）是矩形，      --------------1分

 又 -------------2分

                   -------------3分

 CD            -------------4分

   （II）由，及（I）结论可知DA、DC、DS

两两互相垂直，

建立如图所示的空间直角坐标系

                --------------5分

          _{高☆考♂资♀源*网}                  --------------6分

                     --------------7分

       AD与SB所成的角的余弦为                 --------------8分

   （III）设面SBD的一个法向量为

                --------------9分

    又

∴设面DAB的一个法向量为

所以所求的二面角的余弦为             …………11分

解法二

   （I）同解法一

   （II）矩形ABCD，∴AD//BC，即BC=a，

∴要求AD与SB所成的角，即求BC与SB所成的角    _{高☆考♂资♀源*网}…………5分

在中，由（1）知，SD⊥面ABCD。

中，

CD是CS在面ABCD内的射_{http://www..com/}影，且

                             _{http://www..com/}            --------------6分

              ----------8分

       从而SB与AD的成的角的余弦为

   （III）面ABCD．   BD为面SDB与面ABCD的交线．     SDB      于F，连接EF，      从而得：

为二面角A—SB—D的平面角            ------10分

       在矩形ABCD中，对角线中，

由（2）知在，

而中，SA=a，且AB=2a，

为等腰直角三角形且为直角，

所以所求的二面角的余弦为       _{高☆考♂资♀源*网}           --------------12分