题目内容
4、已知点A,直线a,平面α,①A∈a,a?α?A∉α;②A∈a,a∈α?A∈α;③A∉a,a?α?A∉α;④A∈a,a?α?A?α;以上命题表述正确的真命题的个数是( )
分析:由线面的关系,我们易得直线a,平面α也可能相交于A点,由此可判断①的真假;根据集合与集合关系的描述方法,易判断②的真假;讨论点A,直线a,平面α之间的关系可判断③的真假;根据元素与集合关系的描述方法可判断④的真假.
解答:解:①中,若a∩α=A,则A∈a,a?α成立,但A∉α不成立,故①错误;
②中,若直线a是一个集合,用a∈α描述线面关系不正确,故②错误;
③中,若A是平面α内在直线a外的点,则A∉a,a?α成立,但A∉α不成立,故③错误;
④中,A是一个元素,故用A?α描述点与面的关系不正确,故④错误;
故选A.
②中,若直线a是一个集合,用a∈α描述线面关系不正确,故②错误;
③中,若A是平面α内在直线a外的点,则A∉a,a?α成立,但A∉α不成立,故③错误;
④中,A是一个元素,故用A?α描述点与面的关系不正确,故④错误;
故选A.
点评:本题考查的知识点是元素与集合关系的表示,集合间包含关系的表示,及空间点线面之间的关系,其中用恰当的符号表示元素与集合间、集合与集合间的关系是解答本题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
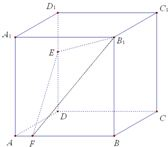 8、如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:①A1C⊥平面B1EF;②△B1EF在侧面BCC1B1上 的正投影是面积为定值的三角形;③在平面A1B1C1D1内总存在与平面B1EF平行的直线;④平 面B1EF与平面ABCD所成的二面角(锐角)的大小与点E的位置有关,与点F的位置无关,其中正确判断的个数有( )
8、如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:①A1C⊥平面B1EF;②△B1EF在侧面BCC1B1上 的正投影是面积为定值的三角形;③在平面A1B1C1D1内总存在与平面B1EF平行的直线;④平 面B1EF与平面ABCD所成的二面角(锐角)的大小与点E的位置有关,与点F的位置无关,其中正确判断的个数有( )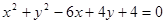 .
. 过点P且与圆心C的距离为1,求直线
过点P且与圆心C的距离为1,求直线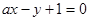 与圆C交于A、B两点,是否存在实数
与圆C交于A、B两点,是否存在实数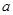 ,使得过点P(2,0)的直线
,使得过点P(2,0)的直线 垂直平
垂直平