题目内容
11.将长为72cm的铁丝截成12段,搭成一个正四棱柱的模型,以此为骨架做成一个容积最大的容器,则此四棱柱的高应该是6cm.分析 设正四棱柱的底面边长为xcm,则正四棱柱的高是$\frac{1}{4}$(72-8x)=18-2x,表示出体积,求导数,即可求出此四棱柱的高.
解答 解:设正四棱柱的底面边长为xcm,则正四棱柱的高是$\frac{1}{4}$(72-8x)=18-2x,
所以体积V=Sh=x2(18-2x)=-2x3+18x2,
求导,得:V'=-6x2+36x=-6x(x-6),
当0<x<6时,V是递增的,当x>6时,V递减,
则x=6cm,18-2x=6cm时,V的最大值是V=216cm3
故答案为:6.
点评 本题考查四棱柱的体积,考查导数知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
20.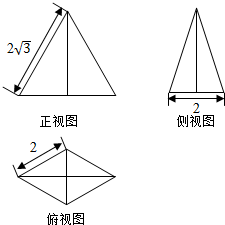 如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
 如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 4$\sqrt{3}$ | D. | 2 |
1.已知集合$A=(-∞,\frac{1}{2}]$,函数y=ln(2x+1)的定义域为集合B,则A∩B=( )
| A. | $({-\frac{1}{2},\frac{1}{2}}]$ | B. | $({-\frac{1}{2},\frac{1}{2}})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $[{\frac{1}{2},+∞})$ |