Question

已知角α,β的终边有下列关系,分别求α,β间的关系式:

(1)α,β的终边关于原点对称;

(2)α,β的终边关于y轴对称.

Answer 1

思路分析:如图.

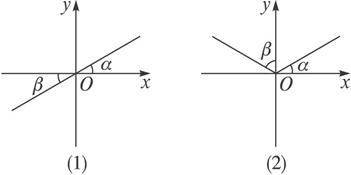
    仔细观察坐标系中α,β的终边位置的关系,适当地变换其中一个角,使两角终边共线,以便用数量关系表示出.

解:(1)由于α,β的终边互为反向延长线,故α,β相差180°的奇数倍〔如图(1)〕.

于是α-β=(2k-1)·180°(k∈Z).

(2)在0°—360°间,设α的终边所表示的角为90°-θ,由于α,β关于y轴对称〔如图(2)〕,则β的终边所表示的角为90°+θ.

于是α=90°-θ+k₁·360°(k₁∈Z),

β=90°+θ+k₂·360°(k₂∈Z),

两式相加得α+β=(2k+1)·180°(k∈Z).

温馨提示

    (1)角α,β的终边关于直线y=x对称,则α,β之间满足关系α+β=k·360°+90°(k∈Z).

    (2)角α,β的终边关于直线y=-x对称,则α,β之间满足关系α+β=k·360°+270°,(k∈Z).