题目内容
过抛物线y2=4x的焦点，作倾斜角为α的直线交抛物线于A，B两点，且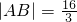
则α=________．
60°或120°
分析：分α=900时，易知不成立，当α≠900时，设直线方程为：y=tanα（x-1），与抛物线方程联立，再由韦达定理和抛物线过焦点的弦长公式求得其倾斜角．
解答：当α=900时，|AB|=4不成立
当α≠900时，设直线方程为：y=tanα（x-1）
与抛物线方程联立得：（tanα）2x2-（2（tanα）2+4）x+（tanα）2=0
∴由韦达定理得：
∴|AB|=x1+x2+p=
∴tanα=±
∴α=600或1200
故答案为：600或1200
点评：本题主要考查直线与抛物线的位置及弦长公式，特别是抛物线过焦点的弦，要灵活地选择公式，提高解题效率．
分析：分α=900时，易知不成立，当α≠900时，设直线方程为：y=tanα（x-1），与抛物线方程联立，再由韦达定理和抛物线过焦点的弦长公式求得其倾斜角．
解答：当α=900时，|AB|=4不成立
当α≠900时，设直线方程为：y=tanα（x-1）
与抛物线方程联立得：（tanα）2x2-（2（tanα）2+4）x+（tanα）2=0
∴由韦达定理得：
∴|AB|=x1+x2+p=
∴tanα=±
∴α=600或1200
故答案为：600或1200
点评：本题主要考查直线与抛物线的位置及弦长公式，特别是抛物线过焦点的弦，要灵活地选择公式，提高解题效率．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
倾斜角为
的直线过抛物线y2=4x的焦点且与抛物线交于A，B两点，则|AB|=（ ）
| π |
| 4 |
A、
| ||
B、8
| ||
| C、16 | ||
| D、8 |
过抛物线y2=4x的焦点F的直线交抛物线于A、B两点，点O是坐标原点，若|AF|=5，则△AOB的面积为（ ）
| A、5 | ||
B、
| ||
C、
| ||
D、
|