题目内容
甲、乙两人各自在300米长的直线形跑道上跑步,则在任一时刻两人在跑道相距不超过50米的概率是
- A.

- B.

- C.
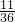
- D.
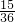
C
分析:设甲、乙两人各自跑的路程,列出不等式,作出图形,再列出相距不超过50米,满足的不等式,求出相应的面积,即可求得相应的概率.
解答: 解:设甲、乙两人各自跑的路程为xm,ym,则
解:设甲、乙两人各自跑的路程为xm,ym,则 ,表示的区域如图所示,面积为90000m2,
,表示的区域如图所示,面积为90000m2,
相距不超过50米,满足|x-y|≤50,表示的区域如图阴影所示,其面积为(90000-62500)m2=27500m2,
∴在任一时刻两人在跑道相距不超过50米的概率是 =
=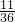
故选C.
点评:解决此类问题的关键是熟练掌握几何概率模型的使用条件,以及几何概率模型的计算公式.
分析:设甲、乙两人各自跑的路程,列出不等式,作出图形,再列出相距不超过50米,满足的不等式,求出相应的面积,即可求得相应的概率.
解答:
 解:设甲、乙两人各自跑的路程为xm,ym,则
解:设甲、乙两人各自跑的路程为xm,ym,则 ,表示的区域如图所示,面积为90000m2,
,表示的区域如图所示,面积为90000m2,相距不超过50米,满足|x-y|≤50,表示的区域如图阴影所示,其面积为(90000-62500)m2=27500m2,
∴在任一时刻两人在跑道相距不超过50米的概率是
 =
=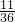
故选C.
点评:解决此类问题的关键是熟练掌握几何概率模型的使用条件,以及几何概率模型的计算公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 B.
B.
 C.
C.
 D.
D.
