题目内容
已知数列{ }的前n项和为
}的前n项和为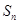 ,且
,且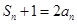 ,则使不等式
,则使不等式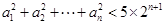 成立的n的最大值为 .
成立的n的最大值为 .
4
解析试题分析:当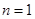 时,
时, ,得
,得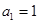 ,
,
当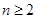 时,
时,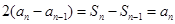 ,所以
,所以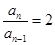 ,所以
,所以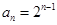 ,
,
又因为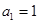 适合上式,所以
适合上式,所以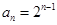 ,所以
,所以 ,
,
所以数列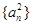 是以
是以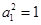 为首项,以4为公比的等比数列,
为首项,以4为公比的等比数列,
所以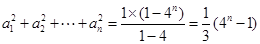 ,
,
所以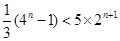 ,即
,即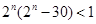 ,易知
,易知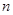 的最大值为4.
的最大值为4.
考点:1.等比数列的求和公式;2.数列的通项公式.

练习册系列答案
相关题目
题目内容
已知数列{ }的前n项和为
}的前n项和为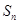 ,且
,且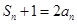 ,则使不等式
,则使不等式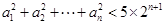 成立的n的最大值为 .
成立的n的最大值为 .
4
解析试题分析:当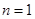 时,
时, ,得
,得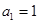 ,
,
当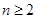 时,
时,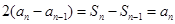 ,所以
,所以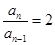 ,所以
,所以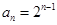 ,
,
又因为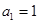 适合上式,所以
适合上式,所以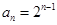 ,所以
,所以 ,
,
所以数列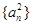 是以
是以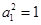 为首项,以4为公比的等比数列,
为首项,以4为公比的等比数列,
所以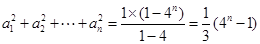 ,
,
所以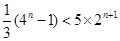 ,即
,即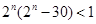 ,易知
,易知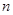 的最大值为4.
的最大值为4.
考点:1.等比数列的求和公式;2.数列的通项公式.
