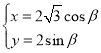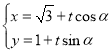题目内容
【题目】已知![]() 是定义在
是定义在![]() 上的函数,记
上的函数,记![]() ,
,![]() 的最大值为
的最大值为![]() .若存在
.若存在![]() ,满足
,满足![]()
![]()
![]() ,则称一次函数
,则称一次函数![]() 是
是![]() 的“逼近函数”,此时的
的“逼近函数”,此时的![]() 称为
称为![]() 在
在![]() 上的“逼近确界”.
上的“逼近确界”.
(1)验证:![]() 是
是![]()
![]() 的“逼近函数”;
的“逼近函数”;
(2)已知![]()
![]()
![]()
![]() .若
.若![]() 是
是![]() 的“逼近函数”,求
的“逼近函数”,求![]() 的值;
的值;
(3)已知![]()
![]() 的逼近确界为
的逼近确界为![]() ,求证:对任意常数
,求证:对任意常数![]() ,
,![]() .
.
【答案】(1)见解析,(2)![]() ,
,![]() ,(3)证明见解析
,(3)证明见解析
【解析】
(1)![]() ,
,
因为![]() ,故
,故![]() 的值域为
的值域为![]() ,故
,故![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() 或
或![]() .
.
取![]() ,
,![]() ,
,![]() ,则
,则![]() ,
, ![]() ,
,![]() ,
,
且![]() ,故
,故![]() 是
是![]()
![]() 的“逼近函数”.
的“逼近函数”.
(2)![]() ,
,
因为![]()
![]() 且
且![]() 是
是![]() 的“逼近函数”,
的“逼近函数”,
故![]() 在
在![]() 和
和![]() 取最小值且
取最小值且![]() 在
在![]() 内取最大值
内取最大值![]() .
.
令![]() ,从而
,从而![]() ,令则
,令则
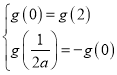 即
即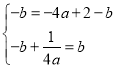 ,故
,故![]() .
.
(3)同(2),![]() ,令
,令![]() ,从而
,从而![]() .
.
因为![]()
![]() 的逼近确界为
的逼近确界为![]() ,
,
由逼近确界的定义可得:存在![]() ,使得
,使得![]() .
.
对于任意的![]() ,
,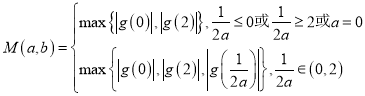 .
.
故![]() 时,有
时,有![]() ,
,
故![]() ,
,
所以![]() ,故
,故![]() .
.
故![]() 时,有
时,有![]() ,
,
故![]() ,
,
所以![]() ,
,
由基本不等式可得![]() ,故
,故![]()
故![]() .
.
综上,对任意的![]() ,有
,有![]() .
.

练习册系列答案
相关题目