题目内容
已知椭圆C1、抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点O,从每条曲线上取两个点,将其坐标记录于下表中:
| x | 1 | - | 2 |  |
| y | 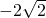 | 0 | -4 |  |
(Ⅱ)过点曲线的C2的焦点B的直线l与曲线C1交于M、N两点,与y轴交于E点,若
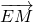 =λ1
=λ1 ,
,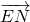 =λ2
=λ2 ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值.
解:(Ⅰ)设抛物线C2:y2=2px,则有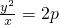 (x≠0),
(x≠0),
据此验证4个点知(1,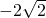 )、(2,-4)在抛物线上,易求y2=8x…(2分)
)、(2,-4)在抛物线上,易求y2=8x…(2分)
设C1: (a>b>0),把点(-
(a>b>0),把点(- ,0)(
,0)( ,
, )代入得:
)代入得: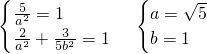 C1方程为
C1方程为 …(5分)
…(5分)
(Ⅱ)证明:设M,N,E点的坐标分别为M(x1,y1)N(x2,y2),E(0,y0),
又易知B点的坐标为(2,0).且点B在椭圆C1内,故过点B的直线l必与椭圆相交.
∵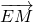 =λ1
=λ1 ,∴(x1,y1-y0)=λ2(2-x1,-y1)
,∴(x1,y1-y0)=λ2(2-x1,-y1)
∴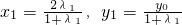 ,. …(8分)
,. …(8分)
将M点坐标代入到椭圆方程中得: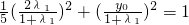 ,
,
去分母整理,得λ12+10λ1+5-5y02=0. …(10分)
同理,由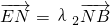 可得:λ22+10λ2+5-5y02=0. …(12分)
可得:λ22+10λ2+5-5y02=0. …(12分)
∴λ1,λ2是方程x2+10x+5-5y02=0的两个根,∴λ1+λ2=10.…(14分)
分析:(Ⅰ)设抛物线C2:y2=2px,则有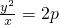 (x≠0),据此验证4个点知(1,
(x≠0),据此验证4个点知(1,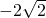 )、(2,-4)在抛物线上可求抛物线方程,设C1:
)、(2,-4)在抛物线上可求抛物线方程,设C1: (a>b>0),把点(-
(a>b>0),把点(- ,0)(
,0)( ,
, )代入可求椭圆方程
)代入可求椭圆方程
(Ⅱ)证明:设M,N,E点的坐标分别为M(x1,y1)N(x2,y2),E(0,y0),B(2,0).由点B在椭圆C1内,故过点B的直线l必与椭圆相交.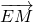 =λ1
=λ1 ,可得(x1,y1-y0)=λ2(2-x1,-y1),将M点坐标代入到椭圆方程可得
,可得(x1,y1-y0)=λ2(2-x1,-y1),将M点坐标代入到椭圆方程可得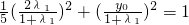 ,由
,由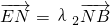 同理可求,从而可求
同理可求,从而可求
点评:本题主要考查了抛物线的方程及椭圆方程的求解,直线与椭圆的位置关系的应用,考查了计算的能力.
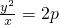 (x≠0),
(x≠0),据此验证4个点知(1,
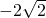 )、(2,-4)在抛物线上,易求y2=8x…(2分)
)、(2,-4)在抛物线上,易求y2=8x…(2分)设C1:
 (a>b>0),把点(-
(a>b>0),把点(- ,0)(
,0)( ,
, )代入得:
)代入得: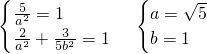 C1方程为
C1方程为 …(5分)
…(5分)(Ⅱ)证明:设M,N,E点的坐标分别为M(x1,y1)N(x2,y2),E(0,y0),
又易知B点的坐标为(2,0).且点B在椭圆C1内,故过点B的直线l必与椭圆相交.
∵
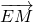 =λ1
=λ1 ,∴(x1,y1-y0)=λ2(2-x1,-y1)
,∴(x1,y1-y0)=λ2(2-x1,-y1)∴
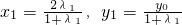 ,. …(8分)
,. …(8分)将M点坐标代入到椭圆方程中得:
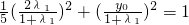 ,
,去分母整理,得λ12+10λ1+5-5y02=0. …(10分)
同理,由
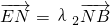 可得:λ22+10λ2+5-5y02=0. …(12分)
可得:λ22+10λ2+5-5y02=0. …(12分)∴λ1,λ2是方程x2+10x+5-5y02=0的两个根,∴λ1+λ2=10.…(14分)
分析:(Ⅰ)设抛物线C2:y2=2px,则有
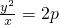 (x≠0),据此验证4个点知(1,
(x≠0),据此验证4个点知(1,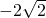 )、(2,-4)在抛物线上可求抛物线方程,设C1:
)、(2,-4)在抛物线上可求抛物线方程,设C1: (a>b>0),把点(-
(a>b>0),把点(- ,0)(
,0)( ,
, )代入可求椭圆方程
)代入可求椭圆方程(Ⅱ)证明:设M,N,E点的坐标分别为M(x1,y1)N(x2,y2),E(0,y0),B(2,0).由点B在椭圆C1内,故过点B的直线l必与椭圆相交.
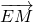 =λ1
=λ1 ,可得(x1,y1-y0)=λ2(2-x1,-y1),将M点坐标代入到椭圆方程可得
,可得(x1,y1-y0)=λ2(2-x1,-y1),将M点坐标代入到椭圆方程可得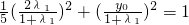 ,由
,由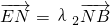 同理可求,从而可求
同理可求,从而可求点评:本题主要考查了抛物线的方程及椭圆方程的求解,直线与椭圆的位置关系的应用,考查了计算的能力.

练习册系列答案
相关题目
已知椭圆C1、抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点O,从每条曲线上取两个点,将其坐标记录于下表中:
则C1、C2的标准方程分别为 、 .
| C1 | C2 | |||||||||
| x | 2 |
|
4 | 3 | ||||||
| y | 0 |
|
4 | -2
| ||||||