题目内容
如图，已知PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点.
(1)求证:MN∥平面PAD;
(2)求证:MN⊥CD;
(3)当∠PDA=45°时,求证:MN⊥平面PCD.
证明:如图，(1)取PD的中点E,连结AE、EN, 有EN ∴四边形AMNE为平行四边形. ∴MN∥AE.又AE ∴MN∥平面PAD. (2)∵PA⊥平面ABCD, ∴PA⊥AB. 又AD⊥AB, ∴AB⊥平面PAD. ∴AB⊥AE,即AB⊥MN.又CD∥AB, ∴MN⊥CD. (3)∵PA⊥平面ABCD, ∴PA⊥AD. 又∠PDA=45°,E为PD的中点, ∴AE⊥PD,即MN⊥PD.又MN⊥CD, ∴MN⊥平面PCD.
CD
AB
AM,
平面PAD,MN
平面PAD,
练习册系列答案
夺冠训练归类模拟总复习系列答案
天府优学系列答案
小升初模拟冲刺卷系列答案
新考题大集结系列答案
中学英语听读导航系列答案
同步宝典1线超越系列答案
海东青中考总复习系列答案
学成教育系统总复习系列答案
全优学习系列答案
名师作业本同步课堂系列答案
相关题目
如图，已知PA⊥矩形ABCD所在平面，M、N分别为AB、PC的中点；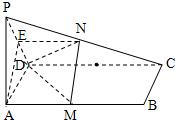
如图，已知PA⊥矩形ABCD所在的平面，M、N分别是AB，PC的中点；若P-CD-A为45°的二面角，求证：平面MND⊥平面PDC；
如图，已知PA⊥矩形ABCD所在平面，M、N分别是AB、PC的中点．
