题目内容
（本小题满分14分）
已知函数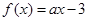
，
，且
.
（1）试求
所满足的关系式；
（2）若
，方程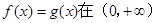
有唯一解，求
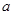的取值范围.
【答案】
（Ⅰ）由
，得
.
所以b、c所满足的关系式为
． …………………………………3分
（Ⅱ）由
，，可得
．
……………………………5分
方程
，即
，可化为
.
令
，则由题意可得，
在
上有唯一解.
令
，由
，可得
.
当
时，由
，可知
是增函数；当
时，由
，可知是减函数．故当时，取极大值
．………………..11分
由函数的图象知，
当
或
时，方程有且仅有一个正实数解．
故所求
的取值范围是
………………………………..14分
【解析】略
练习册系列答案
相关题目
(a＞b＞0)，曲线C2的方程为y=
，且曲线C1与C2在第一象限内只有一个公共点P。（1）试用a表示点P的坐标；（2）设A、B是椭圆C1的两个焦点，当a变化时，求△ABP的面积函数S(a)的值域；（3）记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积，试求函数f(a)=min{g(a), S(a)}的表达式。
=2，点（
）在函数
的图像上，其中
=
.
}是等比数列；
，求
及数列{
}的通项公式；
，求数列{
}的前n项和
，并证明
.
天(
)的销售价格(单位：元)为
，第
，已知该商品成本为每件25元.
关于第
的图像在点
处的切线与直线
平行.
，
满足的关系式；
上恒成立，求
（
）