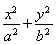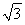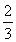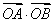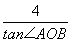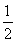题目内容
如图,已知椭圆C: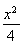 +y2=1,A、B是四条直线x=±2,y=±1所围成的两个顶点.
+y2=1,A、B是四条直线x=±2,y=±1所围成的两个顶点.

(1)设P是椭圆C上任意一点,若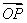 =m
=m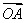 +n
+n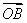 ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
(2)若M、N是椭圆C上两上动点,且直线OM、ON的斜率之积等于直线OA、OB的斜率之积,试探求△OMN的面积是否为定值,说明理由.
(1)见解析(2)1
【解析】(1)易求A(2,1),B(-2,1).(2分)
设P(x0,y0),则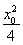 +
+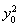 =1.由
=1.由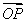 =m
=m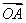 +n
+n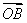 ,,得
,,得
所以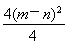 +(m+n)2=1,即m2+n2=
+(m+n)2=1,即m2+n2=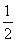 .故点Q(m,n)在定圆x2+y2=
.故点Q(m,n)在定圆x2+y2=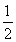 上.(8分)
上.(8分)
(2)设M(x1,y1),N(x2,y2),则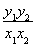 =-
=- .
.
平方得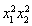 =16
=16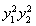 =(4-
=(4-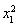 )(4-
)(4-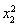 ),即
),即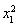 +
+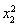 =4.(10分)
=4.(10分)
因为直线MN的方程为(x2-x1)x-(y2-y1)y+x1y2-x2y1=0,
所以O到直线MN的距离为
d=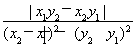 ,(12分)
,(12分)
所以△OMN的面积S=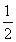 MN·d=
MN·d=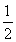 |x1y2-x2y1|=
|x1y2-x2y1|=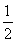
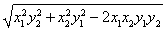
=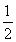
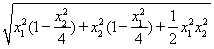 =
=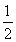
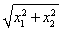 =1.
=1.
故△OMN的面积为定值1.(16分)

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目