题目内容
已知定义在R上的函数f(x),满足对任意a,b∈R,都有f(a+b2)=f(a)+2f2(b)成立,则f(2011)=________.
0或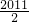
分析:本题利用赋值法解决,令a=b=0得:f(0)=f(0)+2f2(0)?f(0)=0;令a=0,b=1得:f(1)=f(0)+2f2(1)?f(1)=0或f(1)= ,令a=n,b=1得:f(n+1)=f(n)+2f2(1),{f(n)}构成一个等差数列,利用等差数列的通项公式即可求得结果.
,令a=n,b=1得:f(n+1)=f(n)+2f2(1),{f(n)}构成一个等差数列,利用等差数列的通项公式即可求得结果.
解答:令a=b=0得:
f(0)=f(0)+2f2(0)?f(0)=0;
令a=0,b=1得:
f(1)=f(0)+2f2(1)?f(1)=0或f(1)=
令a=n,b=1得:
f(n+1)=f(n)+2f2(1)
当f(1)=0时,
f(n+1)=f(n)
则f(2011)=0;
当f(1)= 时
时
f(n+1)=f(n)+
构成一个等差数列,则f(2011)=f(1)+2010× =
=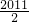
则f(2011)=0或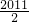
故答案为:0或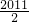 .
.
点评:本题主要考查了抽象函数及其应用,考查了数列的知识.解答的关键是利用赋值法解决问题.
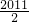
分析:本题利用赋值法解决,令a=b=0得:f(0)=f(0)+2f2(0)?f(0)=0;令a=0,b=1得:f(1)=f(0)+2f2(1)?f(1)=0或f(1)=
 ,令a=n,b=1得:f(n+1)=f(n)+2f2(1),{f(n)}构成一个等差数列,利用等差数列的通项公式即可求得结果.
,令a=n,b=1得:f(n+1)=f(n)+2f2(1),{f(n)}构成一个等差数列,利用等差数列的通项公式即可求得结果.解答:令a=b=0得:
f(0)=f(0)+2f2(0)?f(0)=0;
令a=0,b=1得:
f(1)=f(0)+2f2(1)?f(1)=0或f(1)=

令a=n,b=1得:
f(n+1)=f(n)+2f2(1)
当f(1)=0时,
f(n+1)=f(n)
则f(2011)=0;
当f(1)=
 时
时f(n+1)=f(n)+

构成一个等差数列,则f(2011)=f(1)+2010×
 =
=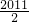
则f(2011)=0或
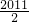
故答案为:0或
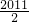 .
.点评:本题主要考查了抽象函数及其应用,考查了数列的知识.解答的关键是利用赋值法解决问题.

练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |