Question

10．如图所示，在三棱锥D-ABC中，AB=BC=CD=1，AC=$\sqrt{3}$，平面ACD⊥平面ABC，∠BCD=90°
（1）求证：CD⊥平面ABC；
（2）求直线BD与平面ACD所成角的正弦值．

Answer 1

分析 （1）过B作BH⊥AC于H，利用平面ACD⊥平面ABC证明BH⊥平面ACD，可得BH⊥CD，利用CD⊥BC，即可证明CD⊥平面ABC；
（2）连接DH，则∠BDH为直线BD与平面ACD所成角，求出BH，BD，即可求直线BD与平面ACD所成角的正弦值．

解答 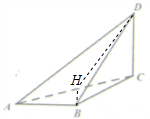（1）证明：过B作BH⊥AC于H，
∵平面ACD⊥平面ABC，平面ACD⊥∩平面ABC=AC
∴BH⊥平面ACD，
∵CD?平面ACD，
∴BH⊥CD，
∵CD⊥BC，BH∩BC=B，
∴CD⊥平面ABC；
（2）解：连接DH，则∠BDH为直线BD与平面ACD所成角．
∵AB=BC=1，AC=$\sqrt{3}$，
∴∠ABC=120°，
∵BH⊥AC，
∴BH=$\frac{1}{2}$，
∵BD=$\sqrt{2}$，
∴sin∠BDH=$\frac{BH}{BD}$=$\frac{\sqrt{2}}{4}$，
∴直线BD与平面ACD所成角的正弦值等于$\frac{\sqrt{2}}{4}$．

点评 本题考查平面与平面垂直的性质，考查线面垂直的判定，考查线面角，考查学生分析解决问题的能力，属于中档题．