题目内容
已知抛物线x2=4y上有一条长为6的动弦AB,则AB中点到x轴的最短距离为( )
A.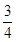 | B. | C.1 | D.2 |
D
易知,AB的斜率存在,设AB方程为y=kx+b.
由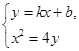 得x2-4kx-4b=0.
得x2-4kx-4b=0.
设A(x1,y1),B(x2,y2),
则x1,x2是上述方程的两个根,
∴x1+x2=4k,x1·x2=-4b,
又|AB|=6,
∴ =6,
=6,
化简得b= -k2,
-k2,
设AB中点为M(x0,y0),
则y0=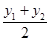 =
= =
= +b
+b
=2k2+ -k2
-k2
=k2+ =(k2+1)+
=(k2+1)+  -1
-1
≥2× -1=2.
-1=2.
当且仅当k2+1= ,
,
即k2=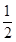 时,y0取到最小值2.故选D.
时,y0取到最小值2.故选D.
由
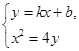 得x2-4kx-4b=0.
得x2-4kx-4b=0.设A(x1,y1),B(x2,y2),
则x1,x2是上述方程的两个根,
∴x1+x2=4k,x1·x2=-4b,
又|AB|=6,
∴
 =6,
=6,化简得b=
 -k2,
-k2,设AB中点为M(x0,y0),
则y0=
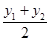 =
= =
= +b
+b=2k2+
 -k2
-k2=k2+
 =(k2+1)+
=(k2+1)+  -1
-1≥2×
 -1=2.
-1=2.当且仅当k2+1=
 ,
,即k2=
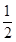 时,y0取到最小值2.故选D.
时,y0取到最小值2.故选D.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
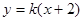 (k>0)与抛物线
(k>0)与抛物线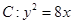 相交于
相交于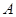 、
、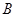 两点,
两点,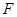 为
为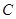 的焦点,若
的焦点,若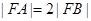 ,则k的值为
,则k的值为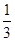
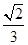
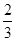
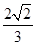
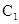 的中心在原点,焦点在x轴上,若
的中心在原点,焦点在x轴上,若 :
: 的焦点重合,且抛物线
的焦点重合,且抛物线 ,则双曲线
,则双曲线

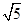 ,则抛物线的方程为( )
,则抛物线的方程为( )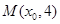 发出的光线,沿平行于抛物线
发出的光线,沿平行于抛物线 的对称轴方向射向此抛物线上的点
的对称轴方向射向此抛物线上的点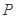 ,经抛物线反射后,穿过焦点射向抛物线上的点
,经抛物线反射后,穿过焦点射向抛物线上的点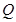 ,再经抛物线反射后射向直线
,再经抛物线反射后射向直线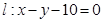 上的点
上的点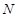 ,经直线反射后又回到点
,经直线反射后又回到点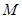 ,则
,则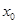 等于( )
等于( )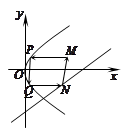




 ),C(x,y),若
),C(x,y),若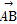 ⊥
⊥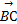 ,则动点C的轨迹方程是_________.
,则动点C的轨迹方程是_________.