题目内容
有一段 “三段论”推理是这样的:对于可导函数 ,若
,若 ,则
,则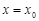 是函数
是函数 的极值点.因为
的极值点.因为 在
在 处的导数值
处的导数值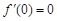 ,所以
,所以 是
是 的极值点.以上推理中 ( )
的极值点.以上推理中 ( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
A
解析试题分析:∵大前提是:“对于可导函数 ,如果
,如果 ,那么
,那么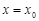 是函数
是函数 的极值点”,不是真命题,因为对于可导函数
的极值点”,不是真命题,因为对于可导函数 ,如果
,如果 ,且满足当x>x0时和当x<x0时的导函数值异号时,那么x=x0是函数f(x)的极值点,∴大前提错误,故选A.
,且满足当x>x0时和当x<x0时的导函数值异号时,那么x=x0是函数f(x)的极值点,∴大前提错误,故选A.
考点:演绎推理的基本方法.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
有一段演绎推理是这样的:“直线平行于平面,则此直线平行于平面内的所有直线;已知直线 平面
平面 ,直线
,直线 平面
平面 ,直线
,直线 平面
平面 ,则直线
,则直线 直线
直线 ”结论显然是错误的,这是因为( )
”结论显然是错误的,这是因为( )
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.非以上错误 |
下列正确的是( )
| A.类比推理是由特殊到一般的推理 |
| B.演绎推理是由特殊到一般的推理 |
| C.归纳推理是由个别到一般的推理 |
| D.合情推理可以作为证明的步骤 |
根据给出的数塔猜测123 456×9+7= ( )
1×9+2=11
12×9+3=111
123×9+4=1 111
1 234×9+5=11 111
12 345×9+6=111 111
……
| A.1 111 110 | B.1 111 111 |
| C.1 111 112 | D.1 111 113 |
 的运算原理如图所示,设
的运算原理如图所示,设
 ,则
,则 上的最小值为 .
上的最小值为 .
 的值是 .
的值是 . 无关)将被执行的次数为 .
无关)将被执行的次数为 . 的值的一个流程图,其中判断
的值的一个流程图,其中判断
 ,可按流程图构造一个数列发生器,其工作原理如下:①输入数据
,可按流程图构造一个数列发生器,其工作原理如下:①输入数据 ,数列发生器输出
,数列发生器输出 ;②若
;②若 ,则数列发生器结束工作;若
,则数列发生器结束工作;若 ,则将
,则将 反馈回输入端再输出
反馈回输入端再输出 ,并且依此规律继续下去.现定义
,并且依此规律继续下去.现定义 .
. ,则由数列发生器产生数列
,则由数列发生器产生数列 ,请写出数列
,请写出数列 的值;
的值; ,均有
,均有 ,求
,求
