题目内容
某种商品每件进价12元,售价20元,每天可卖出48件.若售价降低,销售量可以增加,且售价降低x(0≤x≤8)元时,每天多卖出的件数与x2+x成正比.已知商品售价降低3元时,一天可多卖出36件.
(1)试将该商品一天的销售利润表示成x的函数;
(2)该商品售价为多少元时一天的销售利润最大?
解:(1)由题意可设,每天多卖出的件数为k(x2+x),∴36=k(32+3),∴k=3
又每件商品的利润为(20-12-x)元,每天卖出的商品件数为48+3(x2+x)
∴该商品一天的销售利润为f(x)=(8-x)[48+3(x2+x)]=-3x3+21x2-24x+384(0≤x≤8)
(2)由f'(x)=-9x2+42x-24=-3(x-4)(3x-2)
令f'(x)=0可得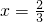 或x=4
或x=4
当x变化时,f'(x)、f(x)的变化情况如下表:
∴当商品售价为16元时,一天销售利润最大,最大值为432元
分析:(1)确定每件商品的利润,每天卖出的商品件数,即可求得该商品一天的销售利润表示成x的函数;
(2)求导函数,确定函数的极值,从而可得最大利润.
点评:本题考查函数模型的构建,考查导数知识的运用,解题的关键是确定函数的解析式.
又每件商品的利润为(20-12-x)元,每天卖出的商品件数为48+3(x2+x)
∴该商品一天的销售利润为f(x)=(8-x)[48+3(x2+x)]=-3x3+21x2-24x+384(0≤x≤8)
(2)由f'(x)=-9x2+42x-24=-3(x-4)(3x-2)
令f'(x)=0可得
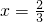 或x=4
或x=4当x变化时,f'(x)、f(x)的变化情况如下表:
| 0 | 4 | 8 | |||||
| - | 0 | + | 0 | - | |||
| 384 | ↘ | 极小值 | ↗ | 极大值432 | ↘ | 0 |
分析:(1)确定每件商品的利润,每天卖出的商品件数,即可求得该商品一天的销售利润表示成x的函数;
(2)求导函数,确定函数的极值,从而可得最大利润.
点评:本题考查函数模型的构建,考查导数知识的运用,解题的关键是确定函数的解析式.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目