题目内容
20.设等差数列{an}的前n项和为Sn,a1=1,S5=45.(1)求数列{an}的通项公式an;
(2)设数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和为Tn,求Tn.
分析 (1)设等差数列的公差为d,运用求和公式,计算可得d=4,再由通项公式即可得到所求;
(2)由$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(4n-3)×(4n+1)}$=$\frac{1}{4n-3}$-$\frac{1}{4n+1}$,由裂项相消求和即可得到所求值.
解答 (1)解:设等差数列的公差为d,
由a1=1,S5=45,可得45=5+$\frac{1}{2}$×5×4d,
解得d=4,
则an=4n-3;
(2)证明:由$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(4n-3)×(4n+1)}$=$\frac{1}{4n-3}$-$\frac{1}{4n+1}$,
则Tn=$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$
=$\frac{1}{1×5}$+$\frac{1}{5×9}$+$\frac{1}{9×13}$+…+$\frac{1}{(4n-3)×(4n+1)}$
=$\frac{1}{4}$(1-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{9}$+$\frac{1}{9}$-$\frac{1}{13}$+…+$\frac{1}{4n-3}$-$\frac{1}{4n+1}$)
=$\frac{1}{4}$(1-$\frac{1}{4n+1}$)=$\frac{n}{4n+1}$.
点评 本题考查等差数列的通项和求和公式的运用,考查数列的求和方法:裂项相消求和,考查运算能力,属于中档题.

练习册系列答案
相关题目
5.已知A={y|y=2x,x∈R},B={y|y=x2,x∈R},则A∩B=( )
| A. | {(0,0),(2,4)} | B. | {0,4} | C. | [0,+∞) | D. | R |
12.下列式子能表示y关于x的函数的是( )
| A. | x+y=3 | B. | y2=2x | C. | y=2x2-x | D. | y2=2x2 |
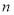 项和为45,前
项和为45,前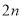 项和为60,则前
项和为60,则前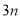 项和为( )
项和为( )