题目内容
 已知函数f (x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,-
已知函数f (x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,- <φ<
<φ< ),其部分图象如所示.将f (x)的图象向右平移2个单位得g(x)的图象,函数g(x)的解析式为
),其部分图象如所示.将f (x)的图象向右平移2个单位得g(x)的图象,函数g(x)的解析式为
- A.g(x)=sin
 (x+1)
(x+1) - B.g(x)=sin
 (x-1)
(x-1) - C.g(x)=sin(
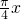 -1)
-1) - D.sin(
 )
)
B
分析:由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,再利用y=Asin(ωx+∅)的变换规律求出函数g(x)的解析式.
解答:由函数f (x)=Asin((ωx+φ)的图象可得,A=1, ,∴ω=
,∴ω= ,
,
∴f (x)=sin( x+φ),再由五点法作图可得
x+φ),再由五点法作图可得  +φ=0,解得 φ=
+φ=0,解得 φ= ,故f (x)=sin(
,故f (x)=sin( x+
x+ ).
).
∵将f (x)的图象向右平移2个单位得g(x)的图象,
∴g(x)=sin[ (x-2)+
(x-2)+ ]=sin
]=sin (x-1).
(x-1).
故选B.
点评:本题主要考查利用y=Asin(ωx+∅)的变换规律,由函数y=Asin(ωx+∅)的部分图象求解析式,属于中档题.
分析:由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,再利用y=Asin(ωx+∅)的变换规律求出函数g(x)的解析式.
解答:由函数f (x)=Asin((ωx+φ)的图象可得,A=1,
 ,∴ω=
,∴ω= ,
,∴f (x)=sin(
 x+φ),再由五点法作图可得
x+φ),再由五点法作图可得  +φ=0,解得 φ=
+φ=0,解得 φ= ,故f (x)=sin(
,故f (x)=sin( x+
x+ ).
).∵将f (x)的图象向右平移2个单位得g(x)的图象,
∴g(x)=sin[
 (x-2)+
(x-2)+ ]=sin
]=sin (x-1).
(x-1).故选B.
点评:本题主要考查利用y=Asin(ωx+∅)的变换规律,由函数y=Asin(ωx+∅)的部分图象求解析式,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|