题目内容
【题目】△ABC中，A(0,1)，AB边上的高CD所在直线的方程为x＋2y－4＝0，AC边上的中线BE所在直线的方程为2x＋y－3＝0.
(1)求直线AB的方程；
(2)求直线BC的方程；
(3)求△BDE的面积．
【答案】（1）
；（2）
；（3）
【解析】试题分析：（1）由
所在直线的方程求出直线
的斜率，再由点斜式写出
的直线方程；
（2）先求出点
，点
的坐标，再写出
的直线方程；
（3）由点到直线的距离求出
到
的距离
，以及
到
的距离
，计算
即可或求出
到
的距离
，计算
.
试题解析：
(1)由已知得直线AB的斜率为2，
∴AB边所在的直线方程为y－1＝2(x－0)，
即2x－y＋1＝0.
(2)由
，得
.
即直线AB与直线BE的交点为B(
，2)．
设C(m，n)，
则由已知条件得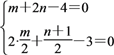
，
解得
，∴C(2,1)．
∴BC边所在直线的方程为
＝
，即2x＋3y－7＝0.
(3)∵E是线段AC的中点，∴E(1,1)．
∴|BE|＝
＝
，
由
，得
.
∴D(
，
)，
∴D到BE的距离为d＝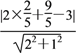
＝
，
∴S△BDE＝·d·|BE|＝
.
练习册系列答案
相关题目
