Question

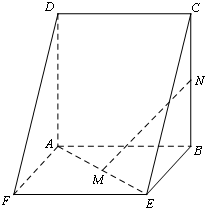如图，边长为4的正方形ABCD与矩形ABEF所在平面互相垂直，M，N分别为AE，BC的中点，AF=3．
（Ⅰ）求证：DA⊥平面ABEF；
（Ⅱ）求证：MN∥平面CDFE．
（Ⅲ）在线段FE上是否存在一点P，使得AP⊥MN？若存在，求出FP的长；若不存在，请说明理由．

Answer 1

分析：（Ⅰ）利用ABCD为正方形，可得DA⊥AB，根据面面垂直的性质，可得DA⊥平面ABEF；
（Ⅱ）连接FB，FC，利用三角形中位线的性质，证明MN∥CF，利用线面平行的判定，可得MN∥平面CDFE；
（Ⅲ）过A点作AG⊥FB交线段于点P，P即为所求，利用△AFP∽△BAF，可求FP的长．

解答：（Ⅰ）证明：因为ABCD为正方形，所以DA⊥AB．
因为正方形ABCD与矩形ABEF所在平面互相垂直，
所以DA⊥平面ABEF；
（Ⅱ）证明：连接FB，FC，则
因为ABEF是矩形，M是AE中点，
所以M是BF的中点，
因为N是BC的中点，
所以MN∥CF，
因为MN?平面CDEF，CF?平面CDEF，
所以MN∥平面CDFE；
（Ⅲ）解：过A点作AG⊥FB交线段于点P，P即为所求．
因为CB⊥平面ABEF，
所以CB⊥AP，
因为AP⊥FB，CB∩FB=B，
所以AP⊥平面BNM，
所以AP⊥MN．
因为△AFP∽△BAF，
所以

FP

AF

=

3

4

，
因为AF=3，
所以FP=

9

4

．

点评：本题考查线面垂直的判定，考查线面平行，考查面面垂直的性质，考查学生分析解决问题的能力，属于中档题．